题目内容

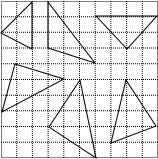如图所示，其中直角三角形的个数为

A.
1个
B.
2个
C.
3个
D.
4个

C
分析：先根据勾股定理判断出三角形的三边长，再由勾股定理的逆定理对各三角形进行逐一判断即可．
解答：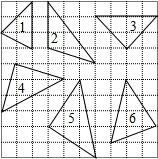

解：在1中，
三角形的三边分别为：2 $\text{[math]}$ ， $\text{[math]}$ ，3，
∵（2 $\text{[math]}$ ）²+（ $\text{[math]}$ ）²=13≠3²，
∴此三角形不是直角三角形；
在2中，
三角形的三边分别为：3， $\text{[math]}$ ，4 $\text{[math]}$ ，
∵3²+（ $\text{[math]}$ ）²=19≠（4 $\text{[math]}$ ）²，
∴此三角形不是直角三角形；
在3中，
三角形的三边分别为：2 $\text{[math]}$ ，2 $\text{[math]}$ ，4，
∵（2 $\text{[math]}$ ）²+（2 $\text{[math]}$ ）²=16=4²，
∴此三角形是直角三角形；
在4中，
三角形的三边分别为： $\text{[math]}$ ， $\text{[math]}$ ，2 $\text{[math]}$ ，
∵（ $\text{[math]}$ ）²+（ $\text{[math]}$ ）²=20=（2 $\text{[math]}$ ）²，
∴此三角形是直角三角形；
在5中，
三角形的三边分别为： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，
∵（ $\text{[math]}$ ）²+（ $\text{[math]}$ ）²=26=（ $\text{[math]}$ ）²，
∴此三角形是直角三角形；
在6中，
三角形的三边分别为： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，
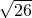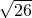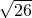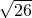∵（ $\text{[math]}$ ）²+（ $\text{[math]}$ ）²=23≠（ $\text{[math]}$ ）²，
∴此三角形不是直角三角形．
故选C．
点评：本题考查的是勾股定理的逆定理及勾股定理，先根据勾股定理判断出各三角形的三边长是解答此题的关键．

练习册系列答案

一考通综合训练系列答案

新课程指导与练习系列答案

中考阶段总复习模拟试题系列答案

全程助学与学习评估系列答案

中考高效复习方案系列答案

走向中考系列答案

甘肃中考试题精选系列答案

中考文言文一本通系列答案

世纪金榜金榜中考系列答案

励耘新中考系列答案

相关题目

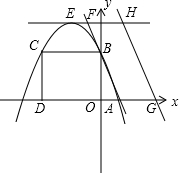矩形OBCD在如图所示的平面直角坐标系中，其中三个顶点分别是O（0，0），B（0，3），D（-2，0），直线AB交x轴于点A（1，0）．
（1）求直线AB的解析式；
（2）求过A、B、C三点的抛物线的解析式，并写出其顶点E的坐标；
（3）过点E作x轴的平行线EF交AB于点F，将直线AB沿x轴向右平移2个单位，与x轴交于点G，与EF交于点H，请问过A、B、C三点的抛物线上是否存在点P，使得S_△PAG=

S_△PEH？若存在，求点P的坐标；若不存在，请说明理由．

19、△ABC在平面直角坐标系中的位置如图所示，其中A，B，C三点的坐标分别为A（4，3），B（3，1），C（1，2）．
（1）作出△ABC关于y轴对称的△A′B′C′；
（2）写出△A′B′C′各顶点的坐标．

梯形ABCD按如图所示放置在直角坐标系中（如图a），AB在x轴上，点D在y轴上，CD∥AB，A（-1，0），C（1，3），抛物线y=-

x2+bx+c经过A、B、D三点，点G是抛物线的顶点，对称轴GH交x轴为H，动点P从点O沿OB以每秒1个单位的速度向终点B运动，设运动时间为t秒．
（1）求抛物线的解析式与线段BC的长度
（2）当t为何值时，△PHG与△AOD相似（点P与点A对应）？
（3）如图（b），连接AC交y轴于点E，动点Q从点B沿BC以每秒1个单位的速度向终点C运动，设点P、Q同时出发，若其中有一点到达终点，则另一点也立即停止运动．
①请探索：是否存在某一时刻t，使△OPQ是以OP为腰的等腰三角形？若存在，求出此时t的值；若不存在，请说明理由．
②如图（c），连接BD交PQ于F，当t=

FD？（请直接写出答案）．

已知一个直三棱柱的三视图的有关尺寸如图所示，其中主视图是以3cm和4cm为直角边的直角三角形，请计算这个几何体的表面积．

矩形OBCD在如图所示的平面直角坐标系中，其中三个顶点分别是O（0，0），B（0，3），D（-2，0），直线AB交x轴于点A（1，0）．
（1）求直线AB的解析式；
（2）求过A、B、C三点的抛物线的解析式，并写出其顶点E的坐标；
（3）过点E作x轴的平行线EF交AB于点F，将直线AB沿x轴向右平移2个单位，与x轴交于点G，与EF交于点H，请问过A、B、C三点的抛物线上是否存在点P，使得S_△PAG=

S_△PEH？若存在，求点P的坐标；若不存在，请说明理由．