题目内容
已知∠B是△ABC中最小的内角,则sinB的取值范围是
- A.0<sinB<

- B.0<sinB≤

- C.0<sinB<

- D.0<sinB≤

D
分析:在三角形中,最小的内角应不大于60度,找到相应的正弦值即可,再根据sin60°= 和一个锐角的正弦值随着角的增大而增大,进行分析.
和一个锐角的正弦值随着角的增大而增大,进行分析.
解答:根据三角形的内角和定理,易知三角形的最小内角不大于60°.
根据题意,知:
0°<∠B≤60°.
又sin60°= ,
,
∴0<n≤ .
.
故选D.
点评:此题主要考查了三角形的内角和定理、特殊角的锐角三角函数值和锐角三角函数值的变化规律,得出0°<∠B≤60°是解题关键.
分析:在三角形中,最小的内角应不大于60度,找到相应的正弦值即可,再根据sin60°=
 和一个锐角的正弦值随着角的增大而增大,进行分析.
和一个锐角的正弦值随着角的增大而增大,进行分析.解答:根据三角形的内角和定理,易知三角形的最小内角不大于60°.
根据题意,知:
0°<∠B≤60°.
又sin60°=
 ,
,∴0<n≤
 .
.故选D.
点评:此题主要考查了三角形的内角和定理、特殊角的锐角三角函数值和锐角三角函数值的变化规律,得出0°<∠B≤60°是解题关键.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
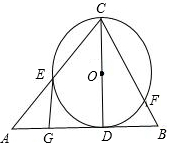 如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O交CA于点E,点G是AD的中点.
如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O交CA于点E,点G是AD的中点.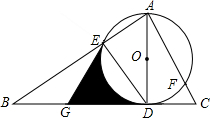 (2013•本溪二模)如图,已知AD是△ABC中BC边上的高,以AD为直径的⊙O分别交AB、AC于点E、F,点G是BD的中点
(2013•本溪二模)如图,已知AD是△ABC中BC边上的高,以AD为直径的⊙O分别交AB、AC于点E、F,点G是BD的中点 如图,已知DC是△ABC中∠ACB的外角平分线,是否可以判定∠BAC与∠B的大小?若能够判定说明理由,不能判定也说明理由.
如图,已知DC是△ABC中∠ACB的外角平分线,是否可以判定∠BAC与∠B的大小?若能够判定说明理由,不能判定也说明理由. 如图,已知DC是△ABC中∠ACB的外角平分线,则有( )
如图,已知DC是△ABC中∠ACB的外角平分线,则有( )