题目内容
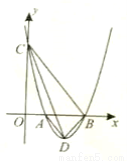
如图,抛物线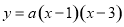 与
与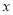 轴交于
轴交于 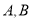 两点,与
两点,与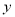 轴的正半轴交于点
轴的正半轴交于点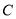 ,其顶点为
,其顶点为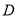 .
.
(1)写出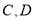 两点的坐标(用含
两点的坐标(用含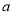 的式子表示);
的式子表示);
(2)设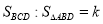 ,求
,求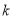 的值;
的值;
(3)当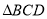 是直角三角形时,求对应抛物线的解析式.
是直角三角形时,求对应抛物线的解析式.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
如图,抛物线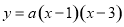 与
与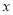 轴交于
轴交于 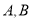 两点,与
两点,与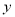 轴的正半轴交于点
轴的正半轴交于点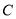 ,其顶点为
,其顶点为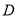 .
.

(1)写出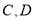 两点的坐标(用含
两点的坐标(用含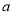 的式子表示);
的式子表示);
(2)设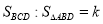 ,求
,求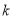 的值;
的值;
(3)当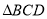 是直角三角形时,求对应抛物线的解析式.
是直角三角形时,求对应抛物线的解析式.
 阅读快车系列答案
阅读快车系列答案