题目内容
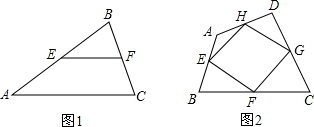
任意四边形ABCD中,点E、F、G、H分别是AD、BC、BD、AC的中点,当四边形ABCD满足条件?????? 时,四边形EGFH是菱形.(填一个使结论成立的条件)
【答案】
AB=CD.
【解析】
试题分析:E、G分别是AD,BD的中点,那么EG就是三角形ADB的中位线,同理,HF是三角形ABC的中位线,因此EG、HF同时平行且相等于AB,因此EG∥HF且EG=HF.因此四边形EHFG是平行四边形,E、H是AD,AC的中点,那么EH= CD,要想证明EHFG是菱形,那么就需证明EG=EH,那么就需要AB、CD满足AB=CD的条件.
CD,要想证明EHFG是菱形,那么就需证明EG=EH,那么就需要AB、CD满足AB=CD的条件.
需添加条件AB=CD.
试题解析:需添加条件AB=CD.
∵点E,G分别是AD,BD的中点,
∴EG∥AB,且EG= AB同理HF∥AB,且HF=
AB同理HF∥AB,且HF= AB,
AB,
∴EG∥HF,EG=HF.
∴四边形EGFH是平行四边形.
∵EG= AB,
AB,
又可同理证得EH= CD,
CD,
∵AB=CD,
∴EG=EH,
∴四边形EGFH是菱形.
故答案为:AB=CD.
考点: 1.菱形的判定;2.三角形中位线定理.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
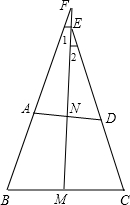 如图,任意四边形ABCD中,AB=CD,M、N分别为BC、AD的中点.说明∠1与∠2的大小关系.
如图,任意四边形ABCD中,AB=CD,M、N分别为BC、AD的中点.说明∠1与∠2的大小关系. 如图任意四边形ABCD中,点E、F、G、H分别是AD、BC、BD、AC的中点,当四边形ABCD满足条件
如图任意四边形ABCD中,点E、F、G、H分别是AD、BC、BD、AC的中点,当四边形ABCD满足条件 (2012•房山区一模)如图,任意四边形ABCD中,AC和BD相交于点O,把△AOB、△AOD、△COD、△BOC的面积分别记作S1、S2、S3、S4,则下列各式成立的是( )
(2012•房山区一模)如图,任意四边形ABCD中,AC和BD相交于点O,把△AOB、△AOD、△COD、△BOC的面积分别记作S1、S2、S3、S4,则下列各式成立的是( )