Question

如图，BD为⊙O的直径，AB=AC，AD交BC于点E，AE=1，ED=2．

（1）求证：∠ABC=∠D；

（2）求AB的长；

（3）延长DB到F，使得BF=BO，连接FA，试判断直线FA与⊙O的位置关系，并说明理由．

Answer 1

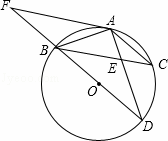
（1）证明：∵AB=AC，

∴∠ABC=∠C，

∵∠C与∠D都对，

∴∠C=∠D，

∴∠ABC=∠D；

（2）解：∵∠ABC=∠D，∠BAE=∠DAB，

∴△ABE∽△ADB，

∴=，即AB²=AE•（AE+ED）=3，

解得：AB=；

（3）答：直线FA与圆O相切．理由如下：

连接OA，

∵BD为圆O的直径，

∴∠BAD=90°，

在Rt△ABD中，AB=，AD=1+2=3，

根据勾股定理得：BD=2，

∴OB=OA=AB=，

∵BF=OB，

∴AB=FB=OB，即AB=OF，

∴∠OAF=90°，

则直线AF与圆O相切．