题目内容
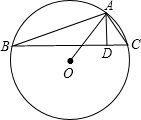在钝角△ABC中，AD⊥BC，垂足为D点，且AD与DC的长度为x2-7x+12=0方程的两个根，⊙O是△ABC的外接圆，如果BD长为a（a＞0）．求△ABC的外接圆⊙O的面积．
分析：要求三角形外接圆的面积，则需要求得该圆的半径．首先运用因式分解的方法解一元二次方程，求得的方程的根即是AD和CD的长；因为AD和CD的大小不确定，所以这里应分情况讨论．要求三角形的外接圆的半径，应作直径，构造直角三角形，根据正弦定理进行求解．
解答：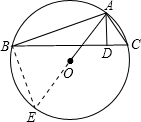
解：延长AO交圆O与点E，连接BE，则∠ABE=90°．
∵AD与DC的长度为一元二次方程x2-7x+12=0的两个根，
∴有两种情况：
①AD=3，DC=4；
②AD=4，DC=3；
在Rt△ADC中，sinC=
，
由正弦定理
=
=
=2R，
可得
=AE，
即AE=
•AC，
当AD=3，DC=4时，
AC=5，
∴AE=
．
⊙O的面积为π•(
)2=
(9+a2)π，
当AD=4，DC=3时，
AB=
，
∴AE=
，
∴⊙O的面积为π•(
)2=
(16+a2)π．
解：延长AO交圆O与点E，连接BE，则∠ABE=90°．∵AD与DC的长度为一元二次方程x2-7x+12=0的两个根，
∴有两种情况：
①AD=3，DC=4；
②AD=4，DC=3；
在Rt△ADC中，sinC=
| AD |
| AC |
由正弦定理
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
可得
| AB |
| sinC |
即AE=
| AB |
| AD |
当AD=3，DC=4时，
AC=5，
∴AE=
| 5 |
| 3 |
| 9+a2 |
⊙O的面积为π•(
| AE |
| 2 |
| 25 |
| 36 |
当AD=4，DC=3时，
AB=
| 16+a2 |
∴AE=
| 5 |
| 4 |
| 16+a2 |
∴⊙O的面积为π•(
| AE |
| 2 |
| 25 |
| 64 |
点评：此题的难点是求三角形外接圆的半径．注意：正弦定理，在△ABC中，
=
=
=2R（R应是三角形的外接圆的半径）．
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
练习册系列答案
阅读快车系列答案
相关题目
17、如图，在钝角△ABC中，点D，E分别是边AC，BC的中点，且DA=DE，那么下列结论错误的是（ ）
26、如图，在钝角△ABC中，点D、E分别是边AC、BC的中点，且DA=DE．有下列结论：①∠1=∠2；②∠1=∠3；③∠B=∠C；④∠B=∠3．其中一定正确的结论有（ ）个．
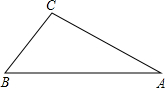如图，在钝角△ABC中，∠A=30°，则tanA的值是（ ）A、
| ||||
B、
| ||||
C、
| ||||
| D、无法确定 |
