题目内容
 如图,⊙O与△ABC的三边分别相切于点D、E、F,连接OB、OC.
如图,⊙O与△ABC的三边分别相切于点D、E、F,连接OB、OC.求证:∠BOC=90°-
| 1 |
| 2 |
考点:切线的性质
专题:证明题
分析:连结OD、OE、OF,如图,根据切线的性质得OD⊥BC,OE⊥AC,OF⊥AB,BF=BD,CE=CD,则根据角平分线性质定理的逆定理得到∠1=∠2,∠3=∠4,则∠BOC=
∠EOF,然后根据四边形的内角和得到∠EOF=180°-∠A,于是有∠BOC=
(180°-∠A)=90°-
∠A.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解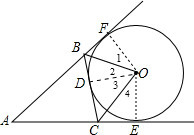 :连结OD、OE、OF,如图,
:连结OD、OE、OF,如图,
∵⊙O与△ABC的三边分别相切于点D、E、F,
∴OD⊥BC,OE⊥AC,OF⊥AB,BF=BD,CE=CD,
∴OB平分∠DOF,OC平分∠DOE,
∴∠1=∠2,∠3=∠4,
∴∠BOC=
∠EOF,
∵∠OEA=∠OFA=90°,
∴∠A+∠EOF=180°,
∴∠EOF=180°-∠A,
∴∠BOC=
(180°-∠A)=90°-
∠A.
 :连结OD、OE、OF,如图,
:连结OD、OE、OF,如图,∵⊙O与△ABC的三边分别相切于点D、E、F,
∴OD⊥BC,OE⊥AC,OF⊥AB,BF=BD,CE=CD,
∴OB平分∠DOF,OC平分∠DOE,
∴∠1=∠2,∠3=∠4,
∴∠BOC=
| 1 |
| 2 |
∵∠OEA=∠OFA=90°,
∴∠A+∠EOF=180°,
∴∠EOF=180°-∠A,
∴∠BOC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系;灵活使用切线长定理.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
下列四个说法中,正确的有( )个.①三个角都相等的三角形是等边三角形.②有两个角等于60°的三角形是等边三角形.③有一个角是60°的等腰三角形是等边三角形.④有两个角相等的等腰三角形是等边三角形.
| A、0个 | B、1个 | C、2个 | D、3个 |
用直尺和圆规作线段的垂直平分线,下列作法正确的是( )
A、 |
B、 |
C、 |
D、 |
 如图,已知AD=
如图,已知AD=
 如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与x轴交点的横坐标分别为x1、x2,其中-2<x1<-1,0<x2<1,下列结论:
如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与x轴交点的横坐标分别为x1、x2,其中-2<x1<-1,0<x2<1,下列结论: