Question

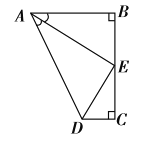
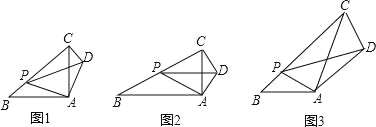
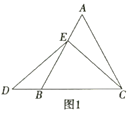
【题目】数学课上,李老师出示了如下的题目：如图1，在等边中，点在上，点在的延长线上，且，试确定线段与的大小关系，并说明理由，

（1）小敏与同桌小聪探究解答的思路如下：

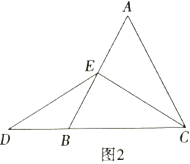
①特殊情况，探索结论，

当点为的中点时，如图2，确定线段与的大小关系，请你直接写出结论：______．(填>，<或=)

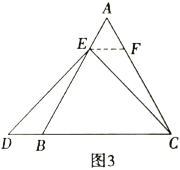
②特例启发，解答题目，

解：题目中，与的大小关系是：______．(填>，<或=)

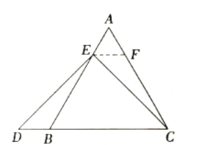
理由如下：如图3，过点作，交于点，(请你补充完成解答过程)

（2）拓展结论，设计新题，

同学小敏解答后，提出了新的问题：在等边中，点在直线上，点在直线上，且，已知的边长为，求的长?(请直接写出结果)

Answer 1

【答案】（1）①AE=DB；②=；理由见解析；（2）2或4．

【解析】

（1）①根据等边三角形性质和等腰三角形的性质求出=求出DB=BE，进而得出AE=DB即可；

②根据题意结合平行线性质利用全等三角形的判定证得△BDE≌△FEC，求出AE=EF进而得到AE=DB即可；

（2）根据题意分两种情况讨论，一种是点在线段上另一种是点在线段的反向延长线上进行分析即可.

解：（1）①∵为等边三角形，点为的中点，

∴, ,

∵,

∴,得出,即有,

∴,

∴AE=DB.

②AE=DB，理由如下：

作EF//BC，交AB于E，AC于F，

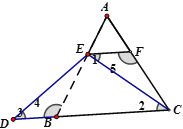
∵EF//BC，

∴∠AEF=∠ABC=60°，∠AFE=∠ACF=60°，∠1=∠2，

∴∠4=∠5=120°，

∵EC=ED，

∴∠2=∠3，

∴∠1=∠3，

在△BDE和△FEC中，，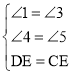

∴△BDE≌△FEC，

∴DB=EF，

∵∠A=∠AEF=∠AFE=60°，

∴△AEF为等边三角形，

∴AE=EF，

∴AE=DB．

(2)第一种情况：

假设点在线段上，并作EF//BC，交AB于E，AC于F，如图所示：

根据②可知AE=DB，

∵在等边中，的边长为，

∴AE=DB=1,

∴;

第二种情况：

假设点在线段的反向延长线上，如图所示：

根据②的结论可知AE=DB，

∵在等边中，的边长为，

∴；

综上所述CD的长为2或4．