题目内容
6.若关于x的一元二次方程-x2+ax+b=0有两个不同的实数根m,n(m<n),方程-x2+ax+b=1有两个不同的实数根p,q(p<q),则m,n,p,q的大小关系为( )| A. | m<p<q<n | B. | p<m<n<q | C. | m<p<n<q | D. | p<m<q<n |
分析 把方程的解理解为抛物线y=-x2+ax+b与x轴两交点坐标为(m,0),(n,0),抛物线y=-x2+ax+b与直线y=1的交点的横坐标分别为p、q,然后画出函数图象后即可得到m,n,p,q的大小关系.
解答 解:∵关于x的一元二次方程-x2+ax+b=0有两个不同的实数根m,n(m<n),
∴抛物线y=-x2+ax+b与x轴两交点坐标为(m,0),(n,0),
∵方程-x2+ax+b=1有两个不同的实数根p,q(p<q),
∴抛物线y=-x2+ax+b与直线y=1的交点的横坐标分别为p、q,
画图: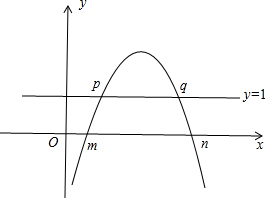
观察图象可得m<p<q<n.
故选A.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程的问题.解决本题的关键是利用函数图象比较m、n、p、q的大小.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
16.一个数的平方等于这个数的4倍,则这个数是( )
| A. | 0 | B. | 4 | C. | 0或4 | D. | 无法确定 |
1.下列说法不正确的是( )
| A. | 绝对值相等的两个有理数,它们的差是0 | |
| B. | 一个有理数减零所得的差是它本身 | |
| C. | 互为相反数的两个有理数,它们的和是0 | |
| D. | 零减去一个有理数所得的差是这个有理数的相反数 |
18.分式$\frac{1}{{a}^{2}-{b}^{2}}$和$\frac{1}{a+b}$的最简公分母是( )
| A. | a+b | B. | a-b | C. | a2-b2 | D. | a2+b2 |
 已知:四边形ABCD中,∠B=∠D=90°,∠A=60°,CD=1,AB=$\sqrt{3}$,求BC、AD的长.
已知:四边形ABCD中,∠B=∠D=90°,∠A=60°,CD=1,AB=$\sqrt{3}$,求BC、AD的长.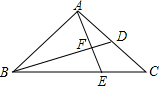 如图,△ABC中,BD平分∠ABC,点E是BC上一点,且满足AB2=BE•BC,AE与BD相交于点F.
如图,△ABC中,BD平分∠ABC,点E是BC上一点,且满足AB2=BE•BC,AE与BD相交于点F.