题目内容
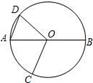
如图12,AB是⊙O的直径,经过圆上点D的直线CD恰使∠ADC=∠B.
(1) 求证:直线CD是⊙O的切线;
(2) 过点A作直线AB的垂线交BD的延长线于点E,且AB=5,BD=2,求线段AE的长.
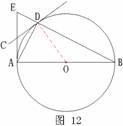
解:(1)证明:连结OD,OD=OB,∠ODB=∠B,
∠ADC=∠B,∠ODB=∠ADC;
∵AB是⊙O的直径,
∴∠ADB=∠ADO+∠ODB=90 º,
∠ADO+∠ADC =90 º,∠ODC=90 º,OD⊥CD,
∴直线CD是⊙O的切线。
(2)AB=5,BD=2,DA=AB2-BD2=1,
∵AE⊥AB,∠EAB=∠ADB=90 º,∠B=∠B,△EAB∽△ADB,
AEDA= ABDB, AE= AB·DADB= 52.
答:线段AE的长为52。

练习册系列答案
相关题目
 =_____.
=_____. 先化简,再求值,
先化简,再求值, 
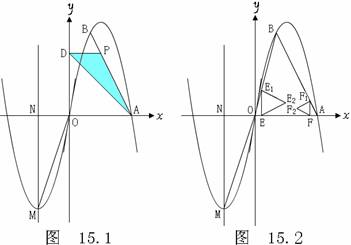 ②过线段OA上的两点E、F分别作x轴的垂线,交折线 O –B -A于点E1、F1,再分别以线段EE1、FF1为边作如图15.2所示的等边△EE1E2、等边△FF1F2,点E以每秒1个单位长度的速度从点O向点A运动,点F以每秒1个单位长度的速度从点A向点O运动,当△EE1E2有一边与△FF1F2的某一边在同一直线上时,求时间t的值.
②过线段OA上的两点E、F分别作x轴的垂线,交折线 O –B -A于点E1、F1,再分别以线段EE1、FF1为边作如图15.2所示的等边△EE1E2、等边△FF1F2,点E以每秒1个单位长度的速度从点O向点A运动,点F以每秒1个单位长度的速度从点A向点O运动,当△EE1E2有一边与△FF1F2的某一边在同一直线上时,求时间t的值. (m2) B、
(m2) B、 (m2) C、1600sinα(m2) D、1600cosα(m2)
(m2) C、1600sinα(m2) D、1600cosα(m2)