题目内容
【题目】如图,己知△ABC中,AB=3,AC=4,BC=5,作∠ABC的角平分线交AC于D,以D为圆心,DA为半径作圆,与射线交于点E、F.有下列结论: ①△ABC是直角三角形;②⊙D与直线BC相切;③点E是线段BF的黄金分割点;④tan∠CDF=2.
其中正确的结论有( )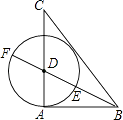
A.4个
B.3个
C.2个
D.1个
【答案】A
【解析】解:∵32+42=52 , ∴AB2+AC2=AB2 ,
∴△ABC是直角三角形,∠BAC=90°,①正确;
作DM⊥BC于M,如图所示:
∵BD是∠ABC的平分线,
∴DM=DA,
∴⊙D与直线BC相切,
∴②正确;
∵∠BAC=∠DMC=90°,
在Rt△BDM和△BDA中,![]() ,
,
∴Rt△BDM≌△BDA(HL),
∴MB=AB=3,
∴CM=BC﹣MB=2,
∵∠C=∠C,
∴△CDM∽△CBA,
∴ ![]() ,即
,即 ![]() ,
,
解得:DM= ![]() ,
,
∴DF=DE= ![]() ,
,
∴BD= ![]() =
= ![]() =
= ![]() ,
,
∴BE=BD﹣DE= ![]() ﹣
﹣ ![]() ,BF=BD+DF=
,BF=BD+DF= ![]() +
+ ![]() ,
,
∵EF2=9,BFBE=( ![]() +
+ ![]() )(
)( ![]() ﹣
﹣ ![]() )=9,
)=9,
∴EF2=BFBE,
∴点E是线段BF的黄金分割点,③正确;
∵tan∠CDF=tan∠ADB= ![]() =
= ![]() =2,
=2,
∴④正确;
正确的有4个.
故选:A.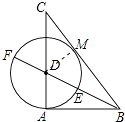
【考点精析】通过灵活运用切线的判定定理和黄金分割,掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;把线段AB分成两条线段AC,BC(AC>BC),并且使AC是AB和BC的比例中项,叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点,其中AC=0.618AB即可以解答此题.

【题目】某体育老师对自己任教的55名男生进行一百米摸底测试,若规定男生成绩为16秒合格,下表是随机抽取的10名男生分A、B两组测试的成绩与合格标准的差值(比合格标准多的秒数为正,少的秒数为负).
A 组 | ﹣1.5 | +1.5 | ﹣1 | ﹣2 | ﹣2 |
B组 | +1 | +3 | ﹣3 | +2 | ﹣3 |
(1)请你估算从55名男生中合格的人数大约是多少?
(2)通过相关的计算,说明哪个组的成绩比较均匀;
(3)至少举出三条理由说明A组成绩好于B组成绩,或找出一条理由来说明B组好于A组.