ЬтФПФкШн
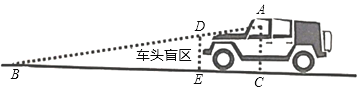
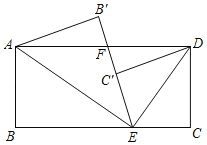
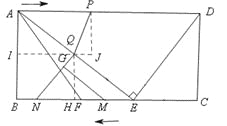
ЁОЬтФПЁПвбжЊЃКдкОиаЮABCDжаЃЌEЮЊБпBCЩЯЕФвЛЕуЃЌAEЁЭDEЃЌAB=12ЃЌBE=16ЃЌFЮЊЯпЖЮBEЩЯвЛЕуЃЌEF=7ЃЌСЌНгAFЃЎШчЭМ1ЃЌЯжгавЛеХгВжНЦЌЁїGMNЃЌЁЯNGM=900ЃЌNG=6ЃЌMG=8ЃЌаББпMNгыБпBCдкЭЌвЛжБЯпЩЯЃЌЕуNгыЕуEжиКЯЃЌЕуGдкЯпЖЮDEЩЯЃЎШчЭМ2ЃЌЁїGMNДгЭМ1ЕФЮЛжУГіЗЂЃЌвдУПУы1ИіЕЅЮЛЕФЫйЖШбиEBЯђЕуBдШЫйвЦЖЏЃЌЭЌЪБЃЌЕуPДгAЕуГіЗЂЃЌвдУПУы1ИіЕЅЮЛЕФЫйЖШбиADЯђЕуDдШЫйвЦЖЏЃЌЕуQЮЊжБЯпGNгыЯпЖЮAEЕФНЛЕуЃЌСЌНгPQЃЎЕБЕуNЕНДяжеЕуBЪБЃЌЁїGMNPКЭЕуЭЌЪБЭЃжЙдЫЖЏЃЎЩшдЫЖЏЪБМфЮЊtУыЃЌНтД№ЮЪЬтЃК

ЃЈ1ЃЉдкећИідЫЖЏЙ§ГЬжаЃЌЕБЕуGдкЯпЖЮAEЩЯЪБЃЌЧѓtЕФжЕЃЛ
ЃЈ2ЃЉдкећИідЫЖЏЙ§ГЬжаЃЌЪЧЗёДцдкЕуPЃЌЪЙЁїAPQЪЧЕШбќШ§НЧаЮЃЌШєДцдкЃЌЧѓГіtЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЛ
ЃЈ3ЃЉдкећИідЫЖЏЙ§ГЬжаЃЌЩшЁїGMNгыЁїAEFжиЕўВПЗжЕФУцЛ§ЮЊSЃЌЧыжБНгаДГіSгыtЕФКЏЪ§ЙиЯЕЪНвдМАздБфСПtЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉt=10УыЃЛЃЈ2ЃЉДцдкЃЌt=![]() ЃЌ
ЃЌ![]() Лђ
Лђ![]() УыЃЛЃЈ3ЃЉ
УыЃЛЃЈ3ЃЉ![]() ЃЛ
ЃЛ![]() ЃЛ
ЃЛ![]() ЃЛ
ЃЛ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЙДЙЩЖЈРэЃЌЧѓГіMNЕФГЄЃЌЕуQдЫЖЏЕНAEЩЯЪБЕФОрРыMNЕФГЄЃЌРыДгЖјГ§вдЫйЖШМДЕУtЕФжЕЃЛ
ЃЈ2ЃЉЁїAPQЪЧЕШбќШ§НЧаЮЃЌЗжЮЊШ§жжЧщаЮЃЌашвЊЗжРрЬжТлЃЌБмУтТЉНтЃЎШчД№ЭМ2ЁЂД№ЭМ3ЁЂД№ЭМ4ЫљЪОЃЛ
ЃЈ3ЃЉећИідЫЖЏЙ§ГЬЗжЮЊЫФИіНзЖЮЃЌУПИіНзЖЮжиЕўЭМаЮЕФаЮзДИїВЛЯрЭЌЃЌШчД№ЭМ5-Д№ЭМ8ЫљЪОЃЌЗжБ№ЧѓГіЦфУцЛ§ЕФБэДяЪНЃЎ
НтЃКЃЈ1ЃЉЁпЁЯNGM=900ЃЌNG=6ЃЌMG=8ЃЌЃЌ
ЁргЩЙДЙЩЖЈРэЃЌЕУNM=10ЃЎ
ЕБЕуGдкЯпЖЮAEЩЯЪБЃЌШчЭМЃЌ
ДЫЪБЃЌGGЁф=MN=10ЃЎ
ЁпЁїGMNДгЭМ1ЕФЮЛжУГіЗЂЃЌвдУПУы1ИіЕЅЮЛЕФЫйЖШбиEBЯђЕуBдШЫйвЦЖЏЃЌ
Ёрt=10УыЃЎ
ЃЈ2ЃЉДцдкЗћКЯЬѕМўЕФЕуPЃЎ
дкRtЁїABEжаЃЌAB=12ЃЌBE=16ЃЌгЩЙДЙЩЖЈРэЕУЃКAE=20ЃЎ
ЩшЁЯAEB=ІШЃЌдђsinІШ=![]() ЃЌcosІШ=
ЃЌcosІШ=![]() ЃЎ
ЃЎ
ЁпNE=tЃЌЁрQE=NEcosІШ=![]() tЃЌAQ=AE-QE=20-
tЃЌAQ=AE-QE=20-![]() tЃЎ
tЃЎ
ЁїAPQЪЧЕШбќШ§НЧаЮЃЌгаШ§жжПЩФмЕФЧщаЮЃК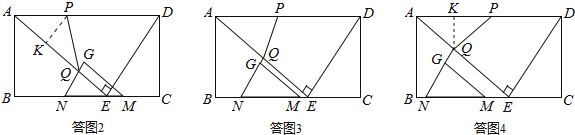
ЂйAP=PQЃЎШчД№ЭМ2ЫљЪОЃК
Й§ЕуPзїPKЁЭAEгкЕуKЃЌдђAK=APcosІШ=![]() tЃЎ
tЃЎ
ЁпAQ=2AKЃЌЁр20-![]() t=2ЁС
t=2ЁС![]() tЃЌ
tЃЌ
НтЕУЃКt=![]() ЃЛ
ЃЛ
ЂкAP=AQЃЎШчД№ЭМ3ЫљЪОЃК
гаt=20-![]() tЃЌ
tЃЌ
НтЕУЃКt=![]() ЃЛ
ЃЛ
ЂлAQ=PQЃЎШчД№ЭМ4ЫљЪОЃК
Й§ЕуQзїQKЁЭAPгкЕуKЃЌдђAK=AQcosІШ=ЃЈ20-![]() tЃЉЁС
tЃЉЁС![]() =16-
=16-![]() tЃЎ
tЃЎ
ЁпAP=2AKЃЌЁрt=2ЃЈ16-![]() tЃЉЃЌ
tЃЉЃЌ
НтЕУЃКt=![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃЌЕБt=![]() ЃЌ
ЃЌ![]() Лђ
Лђ![]() УыЪБЃЌДцдкЕуPЃЌЪЙЁїAPQЪЧЕШбќШ§НЧаЮЃЎ
УыЪБЃЌДцдкЕуPЃЌЪЙЁїAPQЪЧЕШбќШ§НЧаЮЃЎ
гЩОиаЮABCDжаЃЌAB=12ЃЌBE=16ЃЌЕУAE=20ЃЎ
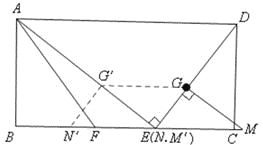
ЂйЕБ0ЃМtЁм10ЪБЃЌЯпЖЮGNгыЯпЖЮAEЯрНЛЃЌШчЭМЃЌЙ§ЕуQзїQHЁЭBCгкЕуHЃЌQIЁЭABгкЕуIЃЌЙ§ЕуPзїPJЁЭIJгкЕуJЃЎ
ИљОнЬтвтЃЌжЊAP=EN=tЃЌ
гЩЁїQNEЁзЁїGNMЕУ![]() ЃЌМД
ЃЌМД![]()
Ёр![]() ЃЌЁр
ЃЌЁр![]() ЃЎ
ЃЎ
гЩЁїQHEЁзЁїNGMЕУ![]() ЃЌМД
ЃЌМД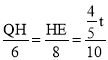 ЃЌ
ЃЌ
Ёр![]()
Ёр![]() ЃЎ
ЃЎ
Ёр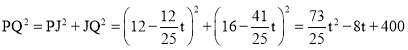 ЃЎ
ЃЎ
ШєAP=AQЃЌдђ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌВЛДцдкЃЛ
ЃЌВЛДцдкЃЛ
ШєAP=PQЃЌдђ![]() ЃЌ
ЃЌ
Ёр![]() ЁїЃМ0ЃЌЮоНтЃЌВЛДцдкЃЛ
ЁїЃМ0ЃЌЮоНтЃЌВЛДцдкЃЛ
ШєAQ=PQЃЌдђ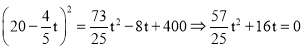 ЃЌЮое§Ъ§НтЃЌВЛДцдкЃЎ
ЃЌЮое§Ъ§НтЃЌВЛДцдкЃЎ
ЂкЕБ10ЃМtЁм16ЪБЃЌЯпЖЮGNЕФбгГЄЯпгыЯпЖЮAEЯрНЛЃЌШчЭМЃЌЙ§ЕуQзїQHЁЭBCгкЕуHЃЌQIЁЭABгкЕуIЃЌЙ§ЕуPзїPJЁЭIJгкЕуJЃЎ
ЭЌЩЯЃЌAP=EN=tЃЌ
гЩЁїQNEЁзЁїGNMЕУ![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
Ёр![]() Ёр
Ёр![]() ЃЎ
ЃЎ
гЩЁїQHEЁзЁїNGMЕУ![]() ЃЌМД
ЃЌМД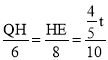 ЃЌ
ЃЌ
Ёр![]()
Ёр![]() ЃЎ
ЃЎ
Ёр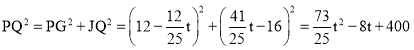 ЃЎ
ЃЎ
ШєAP=AQЃЌдђ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЎ
ЃЎ
ШєAP=PQЃЌдђ![]() ЃЌ
ЃЌ
Ёр![]() ЁїЃМ0ЃЌЮоНтЃЌВЛДцдкЃЛ
ЁїЃМ0ЃЌЮоНтЃЌВЛДцдкЃЛ
ШєAQ=PQЃЌдђ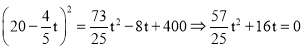 ЃЌЮое§Ъ§НтЃЌВЛДцдкЃЎ
ЃЌЮое§Ъ§НтЃЌВЛДцдкЃЎ
злЩЯЫљЪіЃЌДцдк![]() ЃЌЪЙЁїAPQЪЧЕШбќШ§НЧаЮЃЎ
ЃЌЪЙЁїAPQЪЧЕШбќШ§НЧаЮЃЎ
ЃЈ3ЃЉЕБ0ЃМtЁм7ЪБЃЌЁїGMNгыЁїAEFжиЕўВПЗжЕФУцЛ§ЕШгкЁїQNEЕФУцЛ§ЃЌ
гЩЃЈ2ЃЉЂйЃЌEN=tЃЌ![]() ЃЌЁр
ЃЌЁр![]() ЃЎ
ЃЎ
ЕБ7ЃМtЁм10ЪБЃЌШчЭМЃЌЁїGMNгыЁїAEFжиЕўВПЗжЕФУцЛ§ЕШгкЫФБпаЮQIFEЕФУцЛ§ЃЌЫќЕШгкЁїNQEЕФУцЛ§МѕШЅЁїNIFЕФУцЛ§ЃЎ
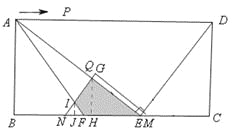
гЩЃЈ2ЃЉЂйЃЌEN=tЃЌ![]() ЃЌЁр
ЃЌЁр![]() ЃЎ
ЃЎ
Й§ЕуI зїIJЁЭBCгкЕуJЃЌ
ЁпEF=7ЃЌEN=tЃЌЁр![]() ЃЎ
ЃЎ
гЩЁїFJIЁзЁїFBAЕУ![]() ЃЌМД
ЃЌМД![]() ЃЎ
ЃЎ
гЩЁїINJЁзЁїMNGЕУ![]() ЃЌМД
ЃЌМД![]() ЃЎ
ЃЎ
ЖўЪНЯрМгЃЌЕУ![]() ЃЎЁр
ЃЎЁр![]()
Ёр![]() ЃЎ
ЃЎ
ЕБ10ЃМtЁм![]() ЪБЃЌШчЭМЃЌЁїGMNгыЁїAEFжиЕўВПЗжЕФУцЛ§ЕШгкЫФБпаЮGIFMЕФУцЛ§ЃЌЫќЕШгкЁїGMNЕФУцЛ§МѕШЅЁїINFЕФУцЛ§ЃЎ
ЪБЃЌШчЭМЃЌЁїGMNгыЁїAEFжиЕўВПЗжЕФУцЛ§ЕШгкЫФБпаЮGIFMЕФУцЛ§ЃЌЫќЕШгкЁїGMNЕФУцЛ§МѕШЅЁїINFЕФУцЛ§ЃЎ
Й§ЕуI зїIHЁЭBCгкЕуHЃЌ
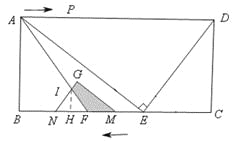
ЁпEF=7ЃЌEN=tЃЌЁр![]() ЃЎ
ЃЎ
гЩЁїFHGЁзЁїFBAЕУ![]() ЃЌМД
ЃЌМД![]() ЃЎ
ЃЎ
гЩЁїINHЁзЁїMNGЕУ![]() ЃЌМД
ЃЌМД![]() ЃЎ
ЃЎ
ЖўЪНЯрМгЃЌЕУ![]() ЃЎЁр
ЃЎЁр![]() ЃЎ
ЃЎ
Ёр![]() ЃЎ
ЃЎ
ЂмЕБ![]() ЃМtЁм16ЪБЪБЃЌШчД№ЭМ8ЫљЪОЃК
ЃМtЁм16ЪБЪБЃЌШчД№ЭМ8ЫљЪОЃК
FM=FE-ME=FE-ЃЈNE-MNЃЉ=17-tЃЎ
ЩшGMгыAFНЛгкЕуIЃЌЙ§ЕуIзїIKЁЭMNгкЕуKЃЎ
ЁпtanЁЯIFK=![]() =
=![]() ЃЌЁрПЩЩшIK=4xЃЌFK=3xЃЌдђKM=3x+17-tЃЎ
ЃЌЁрПЩЩшIK=4xЃЌFK=3xЃЌдђKM=3x+17-tЃЎ
ЁпtanЁЯIMF=![]()
![]() =
=![]() ЃЌ
ЃЌ
НтЕУЃКx=![]() ЃЈ17-tЃЉЃЎ
ЃЈ17-tЃЉЃЎ
ЁрIK=4x=![]() ЃЈ17-tЃЉЃЎ
ЃЈ17-tЃЉЃЎ
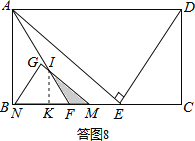
ЁрS=![]() FMIK=
FMIK=![]() ЃЈt-17ЃЉ2ЃЎ
ЃЈt-17ЃЉ2ЃЎ
злЩЯЫљЪіЃЌSгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЮЊЃК![]() ЃЛ
ЃЛ![]() ЃЛ
ЃЛ![]() ЃЛ
ЃЛ![]() ЃЎ
ЃЎ