ĢāÄæÄŚČŻ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬![]()
![]() £¬²¢ĒŅ
£¬²¢ĒŅ![]() Āś×ć
Āś×ć![]() .Ņ»¶Æµć
.Ņ»¶Æµć![]() “Óµć
“Óµć![]() ³ö·¢£¬ŌŚĻ߶Ī
³ö·¢£¬ŌŚĻ߶Ī![]() ÉĻŅŌĆæĆė
ÉĻŅŌĆæĆė![]() øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņµć
øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņµć![]() ŅĘ¶Æ£»¶Æµć
ŅĘ¶Æ£»¶Æµć![]() “Óµć
“Óµć![]() ³ö·¢ŌŚĻ߶Ī
³ö·¢ŌŚĻ߶Ī![]() ÉĻŅŌĆæĆė
ÉĻŅŌĆæĆė![]() øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņµć
øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņµć![]() ŌĖ¶Æ£¬µć
ŌĖ¶Æ£¬µć![]() ·Ö±š“Óµć
·Ö±š“Óµć![]() Ķ¬Ź±³ö·¢£¬µ±µć
Ķ¬Ź±³ö·¢£¬µ±µć![]() ŌĖ¶Æµ½µć
ŌĖ¶Æµ½µć![]() Ź±£¬µć
Ź±£¬µć![]() ĖęÖ®Ķ£Ö¹ŌĖ¶Æ.ÉčŌĖ¶ÆŹ±¼äĪŖ
ĖęÖ®Ķ£Ö¹ŌĖ¶Æ.ÉčŌĖ¶ÆŹ±¼äĪŖ![]() (Ćė)
(Ćė)

(1)Ēó![]() Į½µćµÄ×ų±ź£»
Į½µćµÄ×ų±ź£»
(2)µ±![]() ĪŖŗĪÖµŹ±£¬ĖıߊĪ
ĪŖŗĪÖµŹ±£¬ĖıߊĪ![]() ŹĒĘ½ŠŠĖıߊĪ£æ²¢Ēó³ö“ĖŹ±
ŹĒĘ½ŠŠĖıߊĪ£æ²¢Ēó³ö“ĖŹ±![]() Į½µćµÄ×ų±ź.
Į½µćµÄ×ų±ź.
(3)µ±![]() ĪŖŗĪÖµŹ±£¬
ĪŖŗĪÖµŹ±£¬![]() ŹĒŅŌ
ŹĒŅŌ![]() ĪŖŃüµÄµČŃüČż½ĒŠĪ£æ²¢Ēó³ö“ĖŹ±
ĪŖŃüµÄµČŃüČż½ĒŠĪ£æ²¢Ēó³ö“ĖŹ±![]() Į½µćµÄ×ų±ź.
Į½µćµÄ×ų±ź.
”¾“š°ø”æ(1)![]() £»(2)
£»(2)![]() £»(3)
£»(3) ![]() »ņ
»ņ![]() .
.
”¾½āĪö”æ
(1)Óɶž“ĪøłŹ½ÓŠŅāŅåµÄĢõ¼žæÉĒó³öa”¢bµÄÖµ£¬ŌŁøł¾ŻŅŃÖŖ¼“æÉĒóµĆ“š°ø£»
(2)ÓÉĢāŅāµĆ£ŗ![]() £¬Ōņ
£¬Ōņ![]() £¬µ±
£¬µ±![]() Ź±£¬ĖıߊĪ
Ź±£¬ĖıߊĪ![]() ŹĒĘ½ŠŠĖıߊĪ£¬ÓÉ“ĖæÉµĆ¹ŲÓŚtµÄ·½³Ģ£¬Ēó³ötµÄÖµ¼“æÉĒóµĆ“š°ø£»
ŹĒĘ½ŠŠĖıߊĪ£¬ÓÉ“ĖæÉµĆ¹ŲÓŚtµÄ·½³Ģ£¬Ēó³ötµÄÖµ¼“æÉĒóµĆ“š°ø£»
(3)·Ö![]() ”¢
”¢![]() Į½ÖÖĒéæö·Ö±š»³ö·ūŗĻĢāŅāµÄĶ¼ŠĪ£¬
Į½ÖÖĒéæö·Ö±š»³ö·ūŗĻĢāŅāµÄĶ¼ŠĪ£¬
(1)ÓÉ![]() £¬
£¬
Ōņ![]() £¬
£¬
![]() £¬
£¬
”ßAB//OC£¬A(0£¬12)£¬B(a£¬c)£¬
”ąc=12£¬
”ą![]() £»
£»
(2)ČēĶ¼£¬
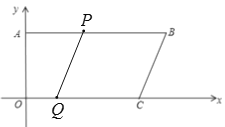
ÓÉĢāŅāµĆ£ŗ![]() £¬
£¬
Ōņ£ŗ![]() £¬
£¬
![]() µ±
µ±![]() Ź±£¬ĖıߊĪ
Ź±£¬ĖıߊĪ![]() ŹĒĘ½ŠŠĖıߊĪ£¬
ŹĒĘ½ŠŠĖıߊĪ£¬
![]() £¬
£¬
½āµĆ£ŗ![]() £¬
£¬
![]() £»
£»
(3)µ±![]() Ź±£¬¹ż
Ź±£¬¹ż![]() ×÷
×÷![]() £¬ŌņĖıߊĪAOQNŹĒ¾ŲŠĪ£¬
£¬ŌņĖıߊĪAOQNŹĒ¾ŲŠĪ£¬
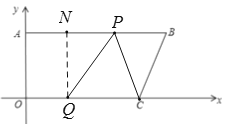
”ąAN=OQ=t£¬QN=OA=12£¬
”ąPN=t£¬
ÓÉĢāŅāµĆ£ŗ![]() £¬
£¬
½āµĆ£ŗ![]() £¬
£¬
¹Ź![]() £¬
£¬
µ±![]() Ź±£¬¹ż
Ź±£¬¹ż![]() ×÷
×÷![]() Öį£¬
Öį£¬

ÓÉĢāŅāµĆ£ŗ![]() £¬
£¬
Ōņ![]() £¬
£¬
½āµĆ£ŗ![]() £¬
£¬
¹Ź![]() .
.