题目内容
12. 如图,已知在△ABC中,∠ABC与∠ACB的平分线交于点P.
如图,已知在△ABC中,∠ABC与∠ACB的平分线交于点P.(1)试比较∠A与∠BPC的大小.
(2)当∠A=α时,求∠BPC的度数.
分析 (1)连接AP并延长至D,根据三角形的外角性质,得出∠BPD+∠CPD>∠BAP+∠CAP,即可得到∠A与∠BPC的大小关系;
(2)先根据∠A=α,∠ABC与∠ACB的角平分线相交于P,求得∠PBC+∠PCB的度数,最后根据三角形内角和定理,求得∠BPC的度数.
解答 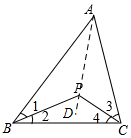 解:(1)连接AP并延长至D,
解:(1)连接AP并延长至D,
∵∠BPD是△ABP的外角,
∴∠BPD>∠BAP,
同理可得,∠CPD>∠CAP,
∴∠BPD+∠CPD>∠BAP+∠CAP,
∴∠BPC>∠BAC;
(2)∵∠A=α,
∴∠ABC+∠ACB=180°-α,
∵∠ABC与∠ACB的角平分线相交于P,
∴∠PBC+∠PCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×(180°-α),
在△PBC中,∠BPC=180°-(∠PBC+∠PCB)=180°-$\frac{1}{2}$×(180°-α)=90°+$\frac{1}{2}$α.
点评 本题主要考查了三角形内角和定理以及三角形外角性质的综合应用,解题时注意:三角形的一个外角大于和它不相邻的任何一个内角.

练习册系列答案
相关题目
 如图,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,那么点E,F是否关于AD对称?若对称,请说明理由.
如图,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,那么点E,F是否关于AD对称?若对称,请说明理由.