题目内容
 2、如图所示,有一个正方体形的铁丝架,把它的侧棱中点I、J、K、L也用铁丝连上.
2、如图所示,有一个正方体形的铁丝架,把它的侧棱中点I、J、K、L也用铁丝连上.(1)现在一个蚂蚁想沿着铁丝从A点爬到G点,问最近的路线一共有几条?并用字母把这些路线表示出来(用所经过的连接点字母表示,譬如蚂蚁从A点出发,经过I点L点,最后到达H点,这样的路线用AILH表示).
(2)蚂蚁是否可能从A点出发,沿着铁丝经过每一个连接点恰好一次,最后到达G点?如果可能,请找出一条这样的路线;如果不可能,说明为什么?
分析:(1)根据乘法原理来解题,从A点到G做到不重不漏,首先确定与A点相连的节点,与G点相连的节点,再向外扩展找对应点.
(2)用反证法来证明不可能.假设可能,将所有连接点染上黑、白两色,凡与黑点相邻的都是白点,凡与白点相邻的都是黑点.再通过黑白点的奇偶性来进一步验证,与假设矛盾.
(2)用反证法来证明不可能.假设可能,将所有连接点染上黑、白两色,凡与黑点相邻的都是白点,凡与白点相邻的都是黑点.再通过黑白点的奇偶性来进一步验证,与假设矛盾.
解答:解:(1)一共有12条:ABCKG、ABJKG、ABJFG、ADCKG、ADLKG、ADLHG、AIJKG、AIJFG、AILKG、AILHG、AIEFG、AIEHG;
(2)不可能.
用反证法证明.假设可能,那么将所有连接点染上黑、白两色,凡与黑点相邻的都是白点,凡与白点相邻的都是黑点.
若A是白点,则黑白点的分布如下表:

由于A与G都是白点,所以蚂蚁从A点出发,依次经过其它各点,到达G点的路线应为白→黑→白→黑→…→黑→白.其中有奇数个白点,这与图中共有偶数个白点相矛盾.
∴蚂蚁不可能从A点出发沿着铁丝经过每一个连接点恰好一次,最后到达G点.
(2)不可能.
用反证法证明.假设可能,那么将所有连接点染上黑、白两色,凡与黑点相邻的都是白点,凡与白点相邻的都是黑点.
若A是白点,则黑白点的分布如下表:

由于A与G都是白点,所以蚂蚁从A点出发,依次经过其它各点,到达G点的路线应为白→黑→白→黑→…→黑→白.其中有奇数个白点,这与图中共有偶数个白点相矛盾.
∴蚂蚁不可能从A点出发沿着铁丝经过每一个连接点恰好一次,最后到达G点.
点评:本题考查加法原理与乘法原理.注意蚂蚁行走顺序,做到不重不漏,本题实际上运用了排列组合中的乘法原理.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
 如图,帆船A和帆船B在太湖湖面上训练,O为湖面上的一个定点,教练船静候于点O,训练时要求A、B两船始终关于O点对称.以O为原点,建立如图所示的坐标系,x轴、y轴的正方向分别表示正东、正北方向.设A、B两船可近似看成在双曲线y=
如图,帆船A和帆船B在太湖湖面上训练,O为湖面上的一个定点,教练船静候于点O,训练时要求A、B两船始终关于O点对称.以O为原点,建立如图所示的坐标系,x轴、y轴的正方向分别表示正东、正北方向.设A、B两船可近似看成在双曲线y=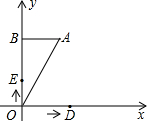 长度的速度沿y轴正方向运动,设D、E两点的运动时间为t秒.
长度的速度沿y轴正方向运动,设D、E两点的运动时间为t秒.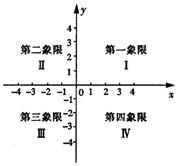
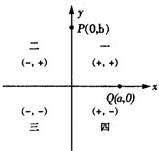
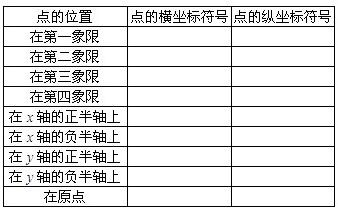
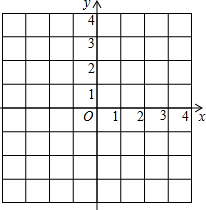 如图,平面直角坐标系中的方格阵表示一个纵横交错的街道模型的一部分,以O为原点,建立如图所示的平面直角坐标系,x轴,y轴的正方向分别表示正东、正北方向,出租车只能沿街道(网格线)行驶,且从一个路口(格点)到另一个路口,必须选择最短路线,称最短路线的长度为两个街区之间的“出租车距离”.设图中每个小正方形方格的边长为1个单位.可以发现:
如图,平面直角坐标系中的方格阵表示一个纵横交错的街道模型的一部分,以O为原点,建立如图所示的平面直角坐标系,x轴,y轴的正方向分别表示正东、正北方向,出租车只能沿街道(网格线)行驶,且从一个路口(格点)到另一个路口,必须选择最短路线,称最短路线的长度为两个街区之间的“出租车距离”.设图中每个小正方形方格的边长为1个单位.可以发现: