题目内容
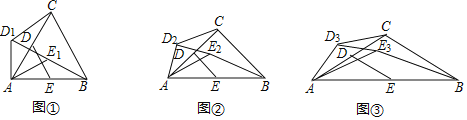
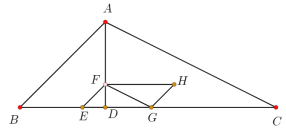
【题目】如图①，在矩形ABCD中，AB＝6，BC＝9，点E是BC边上一动点，连接AE、DE ，作△ECD的外接⊙O，交AD于点F，交AE于点G，连接FG．
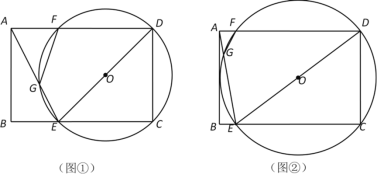
（1）求证△AFG∽△AED；
（2）当BE的长为 时，△AFG为等腰三角形；
（3）如图②，若BE＝1，求证：AB与⊙O相切．
【答案】（1）详见解析；（2）3
、4.5、9－3；（3）详见解析
【解析】
（1）根据圆内接四边形的性质可得∠AGF＝∠ADE，又∠GAF＝∠DAE，从而可证明△AFG∽△AED；
（2）先证明四边形ABEF是矩形，得EF=6，然后分当
时；当
时；当
时三种情况，运用勾股定理求解即可；
（3）连接OM，运用梯形中位线证明OM=OD，
即可．
（1）证明：∵四边形FGED是⊙O的内接四边形，
∴∠AGF＝∠ADE．
又∠GAF＝∠DAE，
∴△AFG∽△AED；
（2）由（1）可知△AFG∽△AED，
∴当△AFG是等腰三角形时，△AED是等腰三角形时，
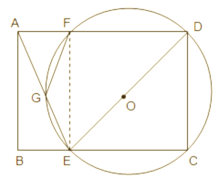
连接EF，如图，
∵四边形ABCD是矩形，
，
，
，
，
是
的外接圆，
是
的直径，
，
，
，
∴四边形
是矩形，
，
是等腰三角形，
∴分三种情况：
①当时，
，
，
又
，
，
；
②当时，
在
中，
，
，
，
，
；
③当时
在
中，
，
，，
综上，当
的长为
或
或
时，
为等腰三角形，
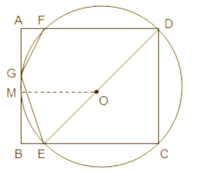
（3）设AB的中点为M，连接OM，如图，
当
时，
，
∵四边形
是矩形，
，
，，
在中，
，
是的直径，
，
∴四边形
是梯形，
又
是AB的中点，O为DE的中点，
是梯形的中位线，
，
，
又
∴AB与相切．
练习册系列答案
相关题目
