题目内容
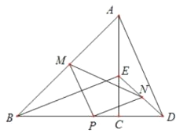
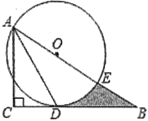
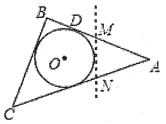
【题目】如图，△ABC是一张周长为18cm的三角形纸片，BC=5cm，⊙O是它的内切圆，小明用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线
剪下△AMN，则剪下的三角形的周长为（ ）
A.
B.
C.
D.随直线的变化而变化
【答案】B
【解析】
如图，设E、F、G分别为⊙O与BC、AC、MN的切点，利用切线长定理得出BC=BD+CF，DM=MG，FN=GN，AD=AF，进而可得答案．
设E、F、G分别为⊙O与BC、AC、MN的切点，
∵⊙O是△ABC的内切圆，
∴BD=BE，CF=CE，AD=AF，
∴BD+CF=BC，
∵MN与⊙O相切于G，
∴DM=MG，FN=GN，
∵△ABC的周长为18cm，BC=5cm，
∴AD+AF=18-BC-(BD+CF)=18-2BC=8cm，
∴△AMN的周长=AM+AN+MG+GN=AM+DM+AN+FN=AD+AF=8cm，
故选：B.
导学与测试系列答案
新非凡教辅冲刺100分系列答案
【题目】为增强中学生体质，篮球运球已列为铜陵市体育中考选考项目，某校学生不仅练习运球，还练习了投篮，下表是一名同学在罚球线上投篮的试验结果，根据表中数据，回答问题．
投篮次数（n） | 50 | 100 | 150 | 200 | 250 | 300 | 500 |
投中次数（m） | 28 | 60 | 78 | 104 | 124 | 153 | 252 |
（1）估计这名同学投篮一次，投中的概率约是多少？（精确到0.1）
（2）根据此概率，估计这名同学投篮622次，投中的次数约是多少？
【题目】采用东阳南枣通过古法熬制而成的蜜枣是我们东阳的土特产之一，已知蜜枣每袋成本10元.试销后发现每袋的销售价
（元）与日销售量
（袋）之间的关系如下表：
| 15 | 20 | 30 | … |
| 25 | 20 | 10 | … |
若日销售量是销售价的一次函数，试求：
（1）日销售量（袋）与销售价（元）的函数关系式.
（2）要使这种蜜枣每日销售的利润最大，每袋的销售价应定为多少元？每日销售的最大利润是多少元？
