题目内容
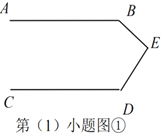
【题目】如图,△ABC中,AD平分∠BAC,
(1)图①中,已知AF⊥BC , ∠B=500,∠C=600. 求∠DAF的度数.
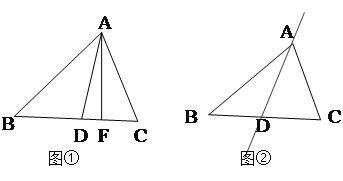
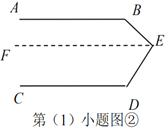
(2)图②中,请你在直线AD上任意取一点E(不与点A、D重合),画EF⊥BC,垂足为F.已知∠B=α,∠C=β(β>a).求∠DEF的度数. (用α、β的代数式表示)
【答案】(1)∠DAF=5°(2)∠DEF=![]() (β-α)
(β-α)
【解析】试题分析:根据三角形的内角和定理可求得∠BAC的度数,又因AD平分∠BAC,根据角平分线的定义可求得∠CAD的度数,再由垂直的定义可得∠AFC的度数,根据直角三角形的两锐角互余即可求得∠DAF的度数;(2)如图2,根据三角形的内角和定理可求得∠BAC的度数,又因AD平分∠BAC,根据角平分线的定义可求得∠CAD的度数,再由三角形的内角和定理求得∠ADC的度数,再由垂直的定义可得∠EFD的度数,根据直角三角形的两锐角互余即可求得∠DEF的度数;如图3,类比图2的方法解决问题即可.
试题解析:
(1)∵∠B=500,∠C=600,
∴∠BAC=180°-∠B-∠C=180°-500-600 =70°,
∵AD平分∠BAC,
∴∠CAD = ![]() ∠BAC =
∠BAC =![]() ×70°=35°,
×70°=35°,
又∵AF⊥BC ,
∴∠AFC =90°,
∴∠CAF =90° -∠C =30°,
∴ ∠DAF =∠CAD -∠CAF =5°.
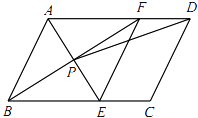
(2)① 如图,

图2
∵∠B=α,∠C=β,
∴∠BAC=180°-∠B-∠C=180°-(α+β),
∵AD平分∠BAC,
∴∠CAD = ![]() ∠BAC =
∠BAC =![]() [180°-(α+β)]=90°-
[180°-(α+β)]=90°-![]() (α+β),
(α+β),
∴∠ADC=180°-∠CAD-∠C=180°-[90°-![]() (α+β)]- β=90°+
(α+β)]- β=90°+![]() α-
α-![]() β
β
又∵EF⊥BC ,
∴∠EFD=90°,
∴∠DEF =90° -∠ADC =90°-[90°+![]() α-
α-![]() β]=
β]= ![]() (β-α).
(β-α).
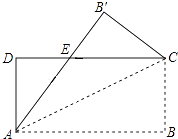
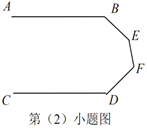
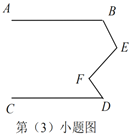
②如图,
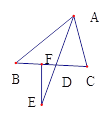
图3
∵∠B=α,∠C=β,
∴∠BAC=180°-∠B-∠C=180°-(α+β),
∵AD平分∠BAC,
∴∠CAD = ![]() ∠BAC =
∠BAC =![]() [180°-(α+β)]=90°-
[180°-(α+β)]=90°-![]() (α+β),
(α+β),
∴∠ADC=180°-∠CAD-∠C=180°-[90°-![]() (α+β)]- β=90°+
(α+β)]- β=90°+![]() α-
α-![]() β
β
∴∠ADC=∠EDF=90°+![]() α-
α-![]() β,
β,
又∵EF⊥BC ,
∴∠EFD=90°,
∴∠DEF =90° -∠EDF =90°-[90°+![]() α-
α-![]() β]=
β]= ![]() (β-α).
(β-α).

 阅读快车系列答案
阅读快车系列答案【题目】一方有难八方支援,某市政府筹集了抗旱必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) |
|
|
|
汽车运费(元/辆) |
|
|
|
(1)若全部物资都用甲、乙两种车型来运送,需运费![]() 元,问分别需甲、乙两种车型各几辆?
元,问分别需甲、乙两种车型各几辆?
(2)为了节约运费,该市政府可以调用甲、乙、丙三种车型参与运送,已知他们的总辆数为![]() 辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
(3)求出哪种方案的运费最省?最省是多少元?