题目内容
如图,Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交斜边AB于点D,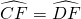 ,连接AF交BC
,连接AF交BC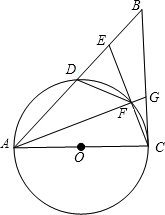 于G,连接CF交AB于E
于G,连接CF交AB于E
(1)求证:DF=EF;
(2)DE=3,FD=5,求⊙O的半径.
(1)证明:∵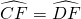 ,∴DF=FC,∠DAF=∠FAC,AC为直径,
,∴DF=FC,∠DAF=∠FAC,AC为直径,
∴∠AFC=∠AFE=90°,
∴△AFE≌△AFC,
∴EF=FC=DF;
(2)解:∵△AFE≌△AFC,EF=FC=DF=5,∴∠FED=∠FDE=∠ACE=∠AEC,
∴△ACE∽△FED,
∴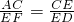 ,
,
可求出AC= ,
,
∴⊙O的半径为 .
.
分析:(1)可证得△AFE≌△AFC,从而得出DF=EF;
(2)由△AFE≌△AFC得出,△ACE∽△FED,则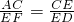 ,从而求出AC=
,从而求出AC= .
.
点评:本题考查了全等三角形的判定和性质以及相似三角形的判定和性质,是基础知识要熟练掌握.
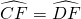 ,∴DF=FC,∠DAF=∠FAC,AC为直径,
,∴DF=FC,∠DAF=∠FAC,AC为直径,∴∠AFC=∠AFE=90°,
∴△AFE≌△AFC,
∴EF=FC=DF;
(2)解:∵△AFE≌△AFC,EF=FC=DF=5,∴∠FED=∠FDE=∠ACE=∠AEC,
∴△ACE∽△FED,
∴
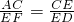 ,
,可求出AC=
 ,
,∴⊙O的半径为
 .
.分析:(1)可证得△AFE≌△AFC,从而得出DF=EF;
(2)由△AFE≌△AFC得出,△ACE∽△FED,则
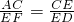 ,从而求出AC=
,从而求出AC= .
.点评:本题考查了全等三角形的判定和性质以及相似三角形的判定和性质,是基础知识要熟练掌握.

练习册系列答案
相关题目

 如图,Rt△ABC中,∠ACB=90°,tanB=
如图,Rt△ABC中,∠ACB=90°,tanB= 如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( )
如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( ) 如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.
如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F. 如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.
如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.