题目内容
 如图,以O为圆心的两个同心圆中,大圆的弦AB切小圆于点C,若∠AOB=120°,小圆半径r=1,则点B到直线AO的距离为( )
如图,以O为圆心的两个同心圆中,大圆的弦AB切小圆于点C,若∠AOB=120°,小圆半径r=1,则点B到直线AO的距离为( )分析:连结OC,作BH⊥AO于H,由大圆的弦AB切小圆于点C,根据切线的性质得OC⊥AB,则根据垂径定理得到AC=BC,易得∠A=30°,然后根据含30度的直角三角形三边的关系求出AC、AB,再得到BH.
解答:解:连结OC,作BH⊥AO于H,如图 ,
,
∵大圆的弦AB切小圆于点C,
∴OC⊥AB,
∴AC=BC,
∵OA=OB,∠AOB=120°,
∴∠A=30°,
在Rt△AOC中,OC=1,AC=
OC=
,
∴AB=2AC=2
,
在Rt△ABH中,BH=
AB=
.
故选C.
 ,
,∵大圆的弦AB切小圆于点C,
∴OC⊥AB,
∴AC=BC,
∵OA=OB,∠AOB=120°,
∴∠A=30°,
在Rt△AOC中,OC=1,AC=
| 3 |
| 3 |
∴AB=2AC=2
| 3 |
在Rt△ABH中,BH=
| 1 |
| 2 |
| 3 |
故选C.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了垂径定理和含30度的直角三角形三边的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 圆于点C,过点C作直线CE⊥AD,垂足为E,交大圆于F,H两点.
圆于点C,过点C作直线CE⊥AD,垂足为E,交大圆于F,H两点. 如图,以O为圆心的两个同心圆中,大圆的弦AB切小圆于P,如果AB=4cm,则图中阴影部分的面积为
如图,以O为圆心的两个同心圆中,大圆的弦AB切小圆于P,如果AB=4cm,则图中阴影部分的面积为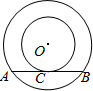 如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,C为切点,若两圆的半径分别为3cm和5cm,则AB的长为
如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,C为切点,若两圆的半径分别为3cm和5cm,则AB的长为 如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,切点为C,若AB=
如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,切点为C,若AB=