Question

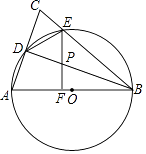
【题目】如图，已知点A，B，C，D，E，F是边长为1的正六边形的顶点，连接任意两点均可得到一条线段．在连接两点所得的所有线段中任取一条线段，取到长度为 的线段的概率为（ ）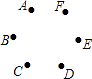

A.
B.
C.
D.

Answer 1

【答案】B
【解析】连接AF，EF，AE，过点F作FN⊥AE于点N，

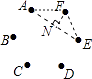
∵点A，B，C，D，E，F是边长为1的正六边形的顶点，

∴AF=EF=1，∠AFE=120°，

∴∠FAE=30°，

∴AN= ，

∴AE= ，同理可得：AC= ，

故从任意一点，连接两点所得的所有线段一共有15种，任取一条线段，取到长度为 的线段有6种情况，

则在连接两点所得的所有线段中任取一条线段，取到长度为 的线段的概率为： ．

故答案为：B．

首先依据正六边形的性质以及勾股定理得出AE=，接下来，确定出所得的线段的总数和长度为的线段的条数，最后再利用概率公式求解即可.