Question

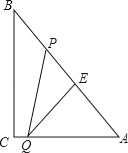
【题目】定义：如图1，D，E在△ABC的边BC上，若△ADE是等边三角形则称△ABC可内嵌，△ADE叫做△ABC的内嵌三角形．

（1）直角三角形______可内嵌．（填写“一定”、“一定不”或“不一定”）

（2）如图2，在△ABC中，∠BAC=120°，△ADE是△ABC的内嵌三角形，试说明AB2=BDBC是否成立？如果成立，请给出证明；如果不一定成立，请举例说明．

（3）在（2）的条件下，如果AB=1，AC=2，求△ABC的内嵌△ADE的边长

Answer 1

【答案】（1）不一定；（2）成立，理由见解析；（3）

【解析】

（1）当直角三角形是等腰直角三角形时可内嵌，所以直角三角形不一定都可内嵌；（2）根据相似三角形的判断方法，得出△BDA∽△BAC，根据相似三角形对应边成比例即可得出；（3）根据△BDA∽△BAC，△AEC∽△BAC，导出DE、CE和x的关系，依据AB2=BDBC列出关于x的方程，从而求出△ABC的内嵌△ADE的边长．

当直角三角形是等腰直角三角形时可内嵌，

∴直角三角形不一定可内嵌.

（2）∵△ADE是△ABC的内嵌三角形，

∴△ADE是正三角形，

∴∠ADE=60°，

在△ADB和△BAC中，

∵∠ADB=∠BAC=120°，∠B=∠B

∴△BDA∽△BAC，

∴,

即AB2=BDBC．

（3）设BD=x，

∵△BDA∽△BAC，

∴ ,

∴

即AD=2x，

∴AE=DE=x

同理可证：△AEC∽△BAC，

∴,

∴

∴CE=4x，

∴BC=7x

由（2）可知AB2=BDBC

∴12=x﹒7x，

解得x=，

∴DE=，

∴△ABC的内嵌△ADE的边长是 ．