题目内容
(2009•雅安)(1)计算:(π-3.14)0-2cos30°+
+(
)-1
(2)先化简代数式:(
-
)•
,然后选取一个合适的x的值,代入求值.
| 27 |
| 1 |
| 2 |
(2)先化简代数式:(
| 3x |
| x-2 |
| x |
| x+2 |
| x2-4 |
| x |
分析:(1)原式第一项利用零指数公式化简,第二项利用特殊角的三角函数值化简,第三项化为最简二次根式,最后一项利用负指数公式化简,合并后即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,分子去括号合并后提取2x,第二个因式的分子利用平方差公式分解因式,约分后得到最简结果,然后取x=1(注意x不能为2,-2,0),将x=1代入化简后的式子中计算,即可得到原式的值.
(2)原式括号中两项通分并利用同分母分式的减法法则计算,分子去括号合并后提取2x,第二个因式的分子利用平方差公式分解因式,约分后得到最简结果,然后取x=1(注意x不能为2,-2,0),将x=1代入化简后的式子中计算,即可得到原式的值.
解答:解:(1)(π-3.14)0-2cos30°+
+(
)-1
=1-2×
+3
+2
=1-
+3
+2
=3+2
;
(2)(
-
)•
=
•
=
•
=2(x+4)
=2x+8,
当x=1时,原式=2+8=10.
| 27 |
| 1 |
| 2 |
=1-2×
| ||
| 2 |
| 3 |
=1-
| 3 |
| 3 |
=3+2
| 3 |
(2)(
| 3x |
| x-2 |
| x |
| x+2 |
| x2-4 |
| x |
=
| 3x(x+2)-x(x-2) |
| (x+2)(x-2) |
| (x+2)(x-2) |
| x |
=
| 2x(x+4) |
| (x+2)(x-2) |
| (x+2)(x-2) |
| x |
=2(x+4)
=2x+8,
当x=1时,原式=2+8=10.
点评:此题考查了分式的化简求值,以及实数的运算,涉及的知识有:零指数、负指数公式,二次根式的化简,特殊角的三角函数值,通分、约分,以及同分母分式的减法法则,熟练掌握公式及法则是解本题的关键.

练习册系列答案
相关题目
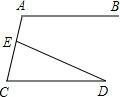 (2009•雅安)如图,AB∥CD,∠A=100°,∠D=25°,则∠AED=( )
(2009•雅安)如图,AB∥CD,∠A=100°,∠D=25°,则∠AED=( )