题目内容
如图,已知抛物线y= (x+2)(x﹣4)与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
(x+2)(x﹣4)与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
(1)求点A、B、C的坐标;
(2)设动点N(﹣2,n),求使MN+BN的值最小时n的值;
(3)P是抛物线上一点,请你探究:是否存在点P,使以P、A、B为顶点的三角形与△ABD相似(△PAB与△ABD不重合)?若存在,求出点P的坐标;若不存在,说明理由.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某市在城中村改造中,需要种植 、
、 两种不同的树苗共
两种不同的树苗共 棵,经招标,承包商以
棵,经招标,承包商以 万元的报价中标承包了这项工程,根据调查及相关资料表明,
万元的报价中标承包了这项工程,根据调查及相关资料表明,  、
、 两种树苗的成本价及成活率如表:
两种树苗的成本价及成活率如表:
品种 | 购买价(元/棵) | 成活率 |
|
|
|
|
|
|
设种植 种树苗
种树苗 棵,承包商获得的利润为
棵,承包商获得的利润为 元.
元.
( )求
)求 与
与 之间的函数关系式.
之间的函数关系式.
( )政府要求栽植这批树苗的成活率不低于
)政府要求栽植这批树苗的成活率不低于 ,承包商应如何选种树苗才能获得最大利润?最大利润是多少?
,承包商应如何选种树苗才能获得最大利润?最大利润是多少?








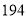 亿立方米.
亿立方米. 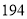 亿用科学记数法表示为( ).
亿用科学记数法表示为( ).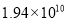 B.
B. 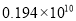 C.
C. 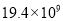 D.
D. 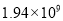
 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( ) B.
B.  C.
C.  D.
D. 