题目内容
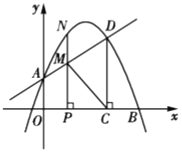
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(-3,2),B(0,-2)其对称轴为直线x=![]() ,C(0,
,C(0, ![]() )为y轴上一点,直线AC与抛物线交于另一点D,
)为y轴上一点,直线AC与抛物线交于另一点D,

(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点F使△ADF是直角三角形,如果存在,求出点F的坐标,如果不存在,请说明理由.
【答案】(1)y=![]() x2-
x2-![]() x-2 ;(2)存在.F点坐标为(
x-2 ;(2)存在.F点坐标为(![]() ,13),(
,13),(![]() ,
,![]() )或(
)或(![]() ,-
,-![]() ),(
),(![]() ,-7).
,-7).
【解析】
(1)根据待定系数法求解即可;
(2)先利用待定系数法求出直线AC的解析式,再和抛物线的解析式联立组成方程组求出点D的坐标,设F(![]() ,m),然后根据两点间的距离公式分别表示出AD2、AF2、DF2,再分三种情况根据勾股定理列出方程,解方程即可求得结果.
,m),然后根据两点间的距离公式分别表示出AD2、AF2、DF2,再分三种情况根据勾股定理列出方程,解方程即可求得结果.
解:(1)由题意得: ,解得
,解得 ,
,
∴抛物线的解析式为y=![]() x2-
x2-![]() x-2 ;
x-2 ;
(2)存在点F使△ADF是直角三角形.
设直线AC的解析式为:![]() ,把A(-3,2)、C(0,
,把A(-3,2)、C(0,![]() )代入,得
)代入,得 ,解得:
,解得: ,∴直线AC的解析式为:
,∴直线AC的解析式为:![]() ,
,
联立方程组 ,解得:
,解得: ,
, ,∴点D坐标为(5,-2),
,∴点D坐标为(5,-2),
设F(![]() ,m),AD2=(5+3)2+(-2-2)2=80,AF2=(
,m),AD2=(5+3)2+(-2-2)2=80,AF2=(![]() +3)2+(m-2)2,DF2=(5-
+3)2+(m-2)2,DF2=(5-![]() )2+(m+2)2,
)2+(m+2)2,
当AD2+DF2=AF2时,△ADF是直角三角形,则80+(5-![]() )2+(m+2)2=(
)2+(m+2)2=(![]() +3)2+(m-2)2,
+3)2+(m-2)2,
解得m=-7,此时F点坐标为(![]() ,-7);
,-7);
当DF2+AF2=AD2时,△ADF是直角三角形,则(5-![]() )2+(m+2)2+(
)2+(m+2)2+(![]() +3)2+(m-2)2=80,
+3)2+(m-2)2=80,
解得m=±![]() ,∴F点坐标为(
,∴F点坐标为(![]() ,
,![]() )或(
)或(![]() ,-
,-![]() );
);
当AD2+AF2=DF2时,△ADF也是直角三角形,则80+(![]() +3)2+(m-2)2=(5-
+3)2+(m-2)2=(5-![]() )2+(m+2)2,
)2+(m+2)2,
解得:m=13,∴F点坐标为(![]() ,13).
,13).
综上,在抛物线的对称轴上存在点F,使△ADF是直角三角形,且F点坐标为(![]() ,13)或(
,13)或(![]() ,
,![]() )或(
)或(![]() ,-
,-![]() )或(
)或(![]() ,-7).
,-7).

【题目】超越公司将某品牌农副产品运往新时代市场进行销售,记汽车行驶时为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
v(千米/小时) | 75 | 80 | 85 | 90 | 95 |
t(小时) | 4.00 | 3.75 | 3.53 | 3.33 | 3.16 |
(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从超越公司出发,能否在上午10:00之前到达新时代市场?请说明理由.