题目内容
 如图,F在平行四边形ABCD的边DC的延长线上,连接AF交BC于E,且CE:BE=1:3,若△EFC的面积等于a,求平行四边形的面积.
如图,F在平行四边形ABCD的边DC的延长线上,连接AF交BC于E,且CE:BE=1:3,若△EFC的面积等于a,求平行四边形的面积.
解:∵DC∥AB,
∴△CEF∽△BEA.
∴ =(
=( )2=
)2= ,
,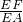 =
= =
= .
.
∴S△ABE=9a,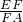 =
= .
.
又∵CE∥AD,
∴△CEF∽△DAF.
∴ =(
=( )2=
)2= =
= .
.
∴S△FAD=16a.
∴SAECD=15a.
SABCD=24a.
分析:根据相似三角形的性质求出△FEC与△FAD的相似比,得到其面积比,再找到△FEC与平行四边形的关系,求出平行四边形的面积.
点评:考查了相似三角形的判定和性质及高相等,平行四边形与梯形面积的关系.
∴△CEF∽△BEA.
∴
 =(
=( )2=
)2= ,
,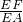 =
= =
= .
.∴S△ABE=9a,
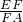 =
= .
.又∵CE∥AD,
∴△CEF∽△DAF.
∴
 =(
=( )2=
)2= =
= .
.∴S△FAD=16a.
∴SAECD=15a.
SABCD=24a.
分析:根据相似三角形的性质求出△FEC与△FAD的相似比,得到其面积比,再找到△FEC与平行四边形的关系,求出平行四边形的面积.
点评:考查了相似三角形的判定和性质及高相等,平行四边形与梯形面积的关系.

练习册系列答案
相关题目
 19、如图,EF在平行四边形ABCD的边AB的延长线上,且EF=AB,DE交CB于点M.
19、如图,EF在平行四边形ABCD的边AB的延长线上,且EF=AB,DE交CB于点M. 如图,F在平行四边形ABCD的边DC的延长线上,连接AF交BC于E,且CE:BE=1:3,若△EFC的面积等于a,求平行四边形的面积.
如图,F在平行四边形ABCD的边DC的延长线上,连接AF交BC于E,且CE:BE=1:3,若△EFC的面积等于a,求平行四边形的面积.

