Question

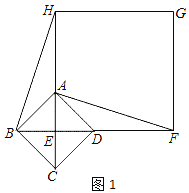
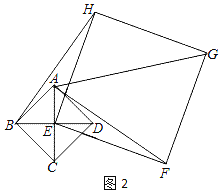
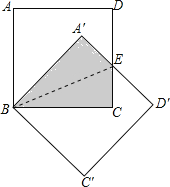
【题目】如图，将边长为2cm的两个互相重合的正方形纸片按住其中一个不动，另一个绕点B顺时针旋转一个角度α（0°＜α＜90°），若两正方形重叠部分的面积为，则这个旋转角度为_____度．

Answer 1

【答案】30°

【解析】分析：设A′D′与CD的交点为E，连接BE；由于A′B=BC，易证得△A′BE≌△CBE，因此两者的面积相等，即可根据△CBE的面积求得CE的值，从而通过解直角三角形求出∠CBE、∠CBA′的度数，进而可求得旋转角的度数．

详解：设A′D′与CD的交点为E，连接BE．

∵A′B=BC，BE=BE，

∴Rt△A′BE≌Rt△CBE．（HL）

∴∠A′BE=∠EBC，且S△BA′E=S△BCE=．

在Rt△BCE中，BC=2，则：

S△BCE=×2×CE=，

∴CE=．

∴tan∠EBC=，即∠EBC=30°．

∴∠A′BC=2∠EBC=60°，∠ABA′=90°-∠A′BC=30°．

故旋转的角度为30°．