题目内容
【题目】在平面直角坐标系中,![]() 为坐标原点,点
为坐标原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,且
,且![]() 满足
满足![]() .
.
(1)若![]() ,判断点
,判断点![]() 处于第几象限,给出你的结论并说明理由;
处于第几象限,给出你的结论并说明理由;
(2)若![]() 为最小正整数,
为最小正整数,![]() 轴上是否存在一点
轴上是否存在一点![]() ,使三角形
,使三角形![]() 的面积等于10,若存在,求点
的面积等于10,若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)点![]() 为坐标系内一点,连接
为坐标系内一点,连接![]() ,若
,若![]() ,且
,且![]() ,直接写出点
,直接写出点![]() 的坐标.
的坐标.
【答案】(1)点![]() 处于第四象限,理由见详解;(2)
处于第四象限,理由见详解;(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根据-a,a的符号和每一象限内点的坐标的性质进行判断;
(2)最小正整数为1,即c=1,代入方程组求出a,b的值,即可确定A、B点的坐标,设点P坐标为![]() ,再根据三角形面积列式计算即可;
,再根据三角形面积列式计算即可;
(3)根据题意画出示意图,根据图示解题即可.
解:(1)∵![]()
∴![]() ,
,
∴![]() ,
,
∴点![]() 处于第四象限;
处于第四象限;
(2)最小正整数为1,即c=1,代入方程组得,
![]() ,解得,
,解得,![]() ,
,
即![]() ,如下图,
,如下图,
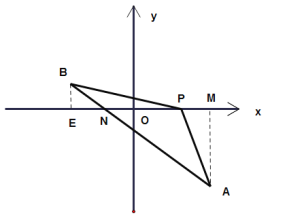
∴直线AB的解解析式为:![]() ,
,
与x轴的交点坐标为N![]() ,
,
设点P的坐标为![]() ,由题意得,
,由题意得,
![]()
解得:![]() 或
或![]()
即点P的坐标为![]() 或
或![]() ;
;
(3)根据题意可画图如下:
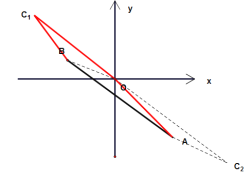
由(2)可知![]() ,
,
∵![]() ,且
,且![]() ,
,
∴四边形![]() ,四边形
,四边形![]() 是平行四边形,
是平行四边形,
当点C位于第二象限时,根据平移的规律可得:![]() ,即
,即![]()
当点C位于第四象限时,根据平移的规律可得:![]() ,即
,即![]()
综上所述点C的坐标为![]() 或
或![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目