题目内容
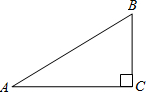
 如图,已知在Rt△ABC中,∠C=90°,CD、CM分别是△ABC的高和中线,DM=1,CD=2,那么△ABC的面积等于________.
如图,已知在Rt△ABC中,∠C=90°,CD、CM分别是△ABC的高和中线,DM=1,CD=2,那么△ABC的面积等于________.

分析:在Rt△CDM中,由勾股定理求CM,根据直角三角形的性质可知AB=2CM,利用S△ABC=
 AB•CD求面积.
AB•CD求面积.解答:∵CD⊥AB,在Rt△CDM中,CD=2,DM=1,
∴CM=
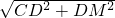 =
= ,在Rt△ABC中,CM为中线,
,在Rt△ABC中,CM为中线,∴AB=2CM=2
 ,
,∴S△ABC=
 AB•CD=
AB•CD= ×2
×2 ×2=2
×2=2 .
.故答案为:2
 .
.点评:本题考查了相似三角形的判定与性质.关键是根据勾股定理求CM,利用直角三角形的性质求AB,从而计算三角形的面积.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 如图,已知在Rt△ABC中,∠C=90°,BC=1,AC=2,则tanA的值为( )
如图,已知在Rt△ABC中,∠C=90°,BC=1,AC=2,则tanA的值为( )| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
 (2012•驿城区模拟)如图,已知在Rt△ABC中,∠B=90°,D、E分别是边AB、AC的中点,若DE=4,AC=10,则AB的值为( )
(2012•驿城区模拟)如图,已知在Rt△ABC中,∠B=90°,D、E分别是边AB、AC的中点,若DE=4,AC=10,则AB的值为( ) 如图,已知在Rt△ABC中,∠C=90°,内切圆的半径为3cm,外接圆的半径为12.5cm,求△ABC的三边长.
如图,已知在Rt△ABC中,∠C=90°,内切圆的半径为3cm,外接圆的半径为12.5cm,求△ABC的三边长. 如图,已知在Rt△ABC中,∠C=90°,点D在BC上,AD=BD,sin∠ADC=
如图,已知在Rt△ABC中,∠C=90°,点D在BC上,AD=BD,sin∠ADC= 如图,已知在Rt△ABC中,∠C=90°.根据要求用尺规作图:
如图,已知在Rt△ABC中,∠C=90°.根据要求用尺规作图: