Question

5．已知△ABC中，AD平分∠BAC交BC于点D，AB=6cm，AC=4cm，且S_△ABC=6cm²，则△ACD的面积为$\frac{12}{5}$cm²．

Answer 1

分析 根据题意画出图形，过点D作DE⊥AB，DF⊥AC，垂足分别为E、F，由角平分线的性质可知DE=DF，根据S_△ABC=6cm²即可得出结论．

解答 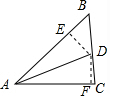解：如图所示，过点D作DE⊥AB，DF⊥AC，垂足分别为E、F，
∵AD平分∠BAC，
∴DE=DF．
∵AB=6cm，AC=4cm，且S_△ABC=6cm²，
∴$\frac{1}{2}$（AB+AC）•DF=6，即$\frac{1}{2}$（6+4）•DF=6，解得DF=$\frac{6}{5}$cm，
∴△ACD的面积=$\frac{1}{2}$AC•DF=$\frac{1}{2}$×4×$\frac{6}{5}$=$\frac{12}{5}$cm²．
故答案为：$\frac{12}{5}$cm²．

点评 本题考查的是角平分线的性质，熟知角的平分线上的点到角的两边的距离相等是解答此题的关键．