题目内容
直线l1经过点(-2,5),并与反比例函数 相交于点P(2,m).
相交于点P(2,m).
(1)求直线l1与反比例函数 的另一个交点的坐标.
的另一个交点的坐标.
(2)把直线l1绕点P按逆时针方向旋转90°得到直线l2,求l2的解析式.
解:(1)∵点P(2,m)在反比例函数图象上,
∴m=3,
∴P(2,3).
设直线l1的解析式为:y=kx+b,由题意,得
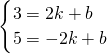 ,
,
解得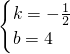 ,
,
∴直线的解析式为:y=- x+4,
x+4,
∴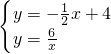 ,
,
解得 ,
,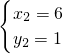 ,
,
∴直线l1与反比例函数 的另一个交点的坐标为(6,1)
的另一个交点的坐标为(6,1)
(2)过点P作x轴的平行线m,过点A作y轴的平行线n交m于点C,
∴PC=4,AC=2,
∵l2⊥l1,设A的对称点为B,过点B作直线a平行于x轴交过点P平行于y轴的直线于点D,由旋转对称得
△PCA≌△PDB,
∴BD=AC=2,PD=PC=4,
∴B(0,-1)
设l2的解析式为y=kx+b,由题意,得
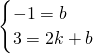 ,
,
解得 ,
,
∴l2的解析式为:y=2x-1.
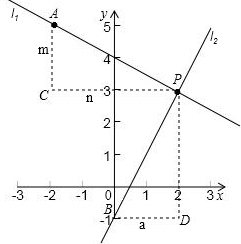
分析:(1)把点P的坐标代入反比例函数的解析式,求出m的值,再利用待定系数法求出直线l1的解析式,再与反比例函数的解析式构成一个方程组求出方程组的解就可以求出另一交点坐标.
(2)根据(1)的结论设A(-2,5),根据旋转对称的性质可以求出A的对称点B的坐标为(0,-1),再利用待定系数法可以求出l2的解析式.
点评:本题是一道反比例函数的综合试题,考查了点的坐标,方程组的解与直线的交点之间的关系,旋转对称的性质,利用待定系数法求直线的解析式.
∴m=3,
∴P(2,3).
设直线l1的解析式为:y=kx+b,由题意,得
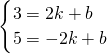 ,
,解得
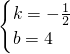 ,
,∴直线的解析式为:y=-
 x+4,
x+4,∴
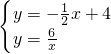 ,
,解得
 ,
,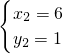 ,
,∴直线l1与反比例函数
 的另一个交点的坐标为(6,1)
的另一个交点的坐标为(6,1)(2)过点P作x轴的平行线m,过点A作y轴的平行线n交m于点C,
∴PC=4,AC=2,
∵l2⊥l1,设A的对称点为B,过点B作直线a平行于x轴交过点P平行于y轴的直线于点D,由旋转对称得
△PCA≌△PDB,
∴BD=AC=2,PD=PC=4,
∴B(0,-1)
设l2的解析式为y=kx+b,由题意,得
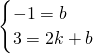 ,
,解得
 ,
,∴l2的解析式为:y=2x-1.

分析:(1)把点P的坐标代入反比例函数的解析式,求出m的值,再利用待定系数法求出直线l1的解析式,再与反比例函数的解析式构成一个方程组求出方程组的解就可以求出另一交点坐标.
(2)根据(1)的结论设A(-2,5),根据旋转对称的性质可以求出A的对称点B的坐标为(0,-1),再利用待定系数法可以求出l2的解析式.
点评:本题是一道反比例函数的综合试题,考查了点的坐标,方程组的解与直线的交点之间的关系,旋转对称的性质,利用待定系数法求直线的解析式.

练习册系列答案
相关题目
探索、研究:下图是按照一定的规律画出的一列“树型”图,下表的n表示“树型”图的序号,an表示第n个“树型”图中“树枝”的个数.
图: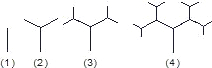
表:
(1)根据“图”、“表”可以归纳出an关于n的关系式为 .
若直线l1经过点(a1,a2)、(a2,a3),求直线l1对应的函数关系式,并说明对任意的正整数n,点(an,an+1)都在直线l1上.
(2)设直线l2:y=-x+4与x轴相交于点A,与直线l1相交于点M,双曲线y=
(x>0)经过点M,且与直线l2相交于另一点N.
①求点N的坐标,并在如图所示的直角坐标系中画出双曲线及直线l1、l2.
②设H为双曲线在点M、N之间的部分(不包括点M、N),P为H上一个动点,点P的横坐标为t,直线MP与x轴相交于点Q,当t为何值时,△MQA的面积等于△PMA的面积的2倍又是否存在t的值,使得△PMA的面积等于1?若存在,求出t的值;若不存在,请说明理由.
③在y轴上是否存在点G,使得△GMN的周长最小?若存在,求出点G的坐标;若不存在,请说明理由.
图:

表:
| n | 1 | 2 | 3 | 4 | … |
| an | 1 | 3 | 7 | 15 | … |
若直线l1经过点(a1,a2)、(a2,a3),求直线l1对应的函数关系式,并说明对任意的正整数n,点(an,an+1)都在直线l1上.
(2)设直线l2:y=-x+4与x轴相交于点A,与直线l1相交于点M,双曲线y=
| k |
| x |
①求点N的坐标,并在如图所示的直角坐标系中画出双曲线及直线l1、l2.
②设H为双曲线在点M、N之间的部分(不包括点M、N),P为H上一个动点,点P的横坐标为t,直线MP与x轴相交于点Q,当t为何值时,△MQA的面积等于△PMA的面积的2倍又是否存在t的值,使得△PMA的面积等于1?若存在,求出t的值;若不存在,请说明理由.
③在y轴上是否存在点G,使得△GMN的周长最小?若存在,求出点G的坐标;若不存在,请说明理由.

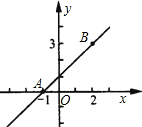 P(m,0).
P(m,0).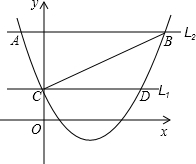
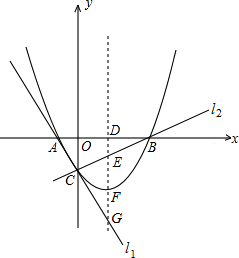 ,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.
,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点. 的坐标是(1,0).
的坐标是(1,0).