题目内容
(2012•毕节地区)如图,直线l1经过点A(-1,0),直线l2经过点B(3,0),l1、l2均为与y轴交于点C(0,-
)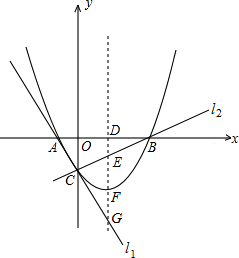 ,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.
,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.
(1)求抛物线的函数表达式;
(2)抛物线的对称轴依次与x轴交于点D、与l2交于点E、与抛物线交于点F、与l1交于点G.求证:DE=EF=FG;
(3)若l1⊥l2于y轴上的C点处,点P为抛物线上一动点,要使△PCG为等腰三角形,请写出符合条件的点P的坐标,并简述理由.
| 3 |
 ,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.
,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.(1)求抛物线的函数表达式;
(2)抛物线的对称轴依次与x轴交于点D、与l2交于点E、与抛物线交于点F、与l1交于点G.求证:DE=EF=FG;
(3)若l1⊥l2于y轴上的C点处,点P为抛物线上一动点,要使△PCG为等腰三角形,请写出符合条件的点P的坐标,并简述理由.
分析:(1)已知A、B、C三点坐标,利用待定系数法求出抛物线的解析式;
(2)D、E、F、G四点均在对称轴x=1上,只要分别求出其坐标,就可以得到线段DE、EF、FG的长度.
D是对称轴与x轴交点,F是抛物线顶点,其坐标易求;E是对称轴与直线l2交点,需要求出l2的解析式,G是对称轴与l1的交点,需要求出l1的解析式,而A、B、C三点坐标已知,所以l1、l2的解析式可以用待定系数法求出.至此本问解决;
(3)△PCG为等腰三角形,需要分三种情况讨论.如解答图所示,在解答过程中,充分注意到△ECG为含30度角的直角三角形,△P1CG为等边三角形,分别利用其几何性质,则本问不难解决.
(2)D、E、F、G四点均在对称轴x=1上,只要分别求出其坐标,就可以得到线段DE、EF、FG的长度.
D是对称轴与x轴交点,F是抛物线顶点,其坐标易求;E是对称轴与直线l2交点,需要求出l2的解析式,G是对称轴与l1的交点,需要求出l1的解析式,而A、B、C三点坐标已知,所以l1、l2的解析式可以用待定系数法求出.至此本问解决;
(3)△PCG为等腰三角形,需要分三种情况讨论.如解答图所示,在解答过程中,充分注意到△ECG为含30度角的直角三角形,△P1CG为等边三角形,分别利用其几何性质,则本问不难解决.
解答:解:(1)抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(3,0),C(0,-
)三点,
∴
,解得a=
,b=-
,c=-
,
∴抛物线的解析式为:y=
x2-
x-
.
(2)设直线l1的解析式为y=kx+b,由题意可知,直线l1经过A(-1,0),C(0,-
)两点,
∴
,解得k=-
,b=-
,∴直线l1的解析式为:y=-
x-
;
直线l2经过B(3,0),C(0,-
)两点,同理可求得直线l2解析式为:y=
x-
.
∵抛物线y=
x2-
x-
=
(x-1)2-
,
∴对称轴为x=1,D(1,0),顶点坐标为F(1,-
);
点E为x=1与直线l2:y=
x-
的交点,令x=1,得y=-
,∴E(1,-
);
点G为x=1与直线l1:y=-
x-
的交点,令x=1,得y=-2
,∴G(1,-2
).
∴各点坐标为:D(1,0),E(1,-
),F(1,-
),G(1,-2
),它们均位于对称轴x=1上,
∴DE=EF=FG=
.
(3)如右图,过C点作C关于对称轴x=1的对称点P1,CP1交对称轴于H点,连接CF.
△PCG为等腰三角形,有三种情况: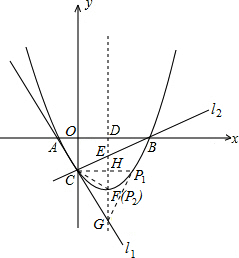
①当CG=PG时,如右图,由抛物线的对称性可知,此时P1满足P1G=CG.
∵C(0,-
),对称轴x=1,∴P1(2,-
).
②当CG=PC时,此时P点在抛物线上,且CP的长度等于CG.
如右图,C(0,-
),H点在x=1上,∴H(1,-
),
在Rt△CHG中,CH=1,HG=|yG-yH|=|-2
-(-
)|=
,
∴由勾股定理得:CG=
=2.
∴PC=2.
如右图,CP1=2,此时与①中情形重合;
又Rt△OAC中,AC=
=2,∴点A满足PC=2的条件,但点A、C、G在同一条直线上,所以不能构成等腰三角形.
③当PC=PG时,此时P点位于线段CG的垂直平分线上.
∵l1⊥l2,∴△ECG为直角三角形,
由(2)可知,EF=FG,即F为斜边EG的中点,
∴CF=FG,∴F为满足条件的P点,∴P2(1,-
);
又cos∠CGE=
=
,∴∠CGE=30°,∴∠HCG=60°,
又P1C=CG,∴△P1CG为等边三角形,
∴P1点也在CG的垂直平分线上,此种情形与①重合.
综上所述,P点的坐标为P1(2,-
)或P2(1,-
).
| 3 |
∴
|
| ||
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
∴抛物线的解析式为:y=
| ||
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
(2)设直线l1的解析式为y=kx+b,由题意可知,直线l1经过A(-1,0),C(0,-
| 3 |
∴
|
| 3 |
| 3 |
| 3 |
| 3 |
直线l2经过B(3,0),C(0,-
| 3 |
| ||
| 3 |
| 3 |
∵抛物线y=
| ||
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| ||
| 3 |
| 4 |
| 3 |
| 3 |
∴对称轴为x=1,D(1,0),顶点坐标为F(1,-
| 4 |
| 3 |
| 3 |
点E为x=1与直线l2:y=
| ||
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
点G为x=1与直线l1:y=-
| 3 |
| 3 |
| 3 |
| 3 |
∴各点坐标为:D(1,0),E(1,-
| 2 |
| 3 |
| 3 |
| 4 |
| 3 |
| 3 |
| 3 |
∴DE=EF=FG=
| 2 |
| 3 |
| 3 |
(3)如右图,过C点作C关于对称轴x=1的对称点P1,CP1交对称轴于H点,连接CF.
△PCG为等腰三角形,有三种情况:

①当CG=PG时,如右图,由抛物线的对称性可知,此时P1满足P1G=CG.
∵C(0,-
| 3 |
| 3 |
②当CG=PC时,此时P点在抛物线上,且CP的长度等于CG.
如右图,C(0,-
| 3 |
| 3 |
在Rt△CHG中,CH=1,HG=|yG-yH|=|-2
| 3 |
| 3 |
| 3 |
∴由勾股定理得:CG=
12+(
|
∴PC=2.
如右图,CP1=2,此时与①中情形重合;
又Rt△OAC中,AC=
12+(
|
③当PC=PG时,此时P点位于线段CG的垂直平分线上.
∵l1⊥l2,∴△ECG为直角三角形,
由(2)可知,EF=FG,即F为斜边EG的中点,
∴CF=FG,∴F为满足条件的P点,∴P2(1,-
| 4 |
| 3 |
| 3 |
又cos∠CGE=
| CG |
| EG |
| ||
| 2 |
又P1C=CG,∴△P1CG为等边三角形,
∴P1点也在CG的垂直平分线上,此种情形与①重合.
综上所述,P点的坐标为P1(2,-
| 3 |
| 4 |
| 3 |
| 3 |
点评:作为中考压轴题,本题考查的知识点比较多,包括二次函数的图象与性质、待定系数法求函数(二次函数、一次函数)解析式、等腰三角形、等边三角形以及勾股定理等.难点在于第(3)问,需要针对等腰三角形△PCG的三种可能情况分别进行讨论,在解题过程中,需要充分挖掘并利用题意隐含的条件(例如直角三角形、等边三角形),这样可以简化解答过程.

练习册系列答案
相关题目

 (2012•毕节地区)如图,双曲线
(2012•毕节地区)如图,双曲线