题目内容
如图1、图2、图3、…、图n分别是⊙O的内接正三角形A1A2A3,正四边形A1A2A3A4、正五边形A1A2A3A4A5、…、正n边形A1A2A3∧An,点M、N分别是弧A1A2和A2A3上的点.且弧A1M=弧A2N,连接AnM、A1N相交于点P,
观察并分析:(1)∠A3PN=________;∠A4PN=________;∠AnPN=________.
60° 90° 
分析:图1中,由三角形外角定理可得∠A3PN的大小等于其一个内角得大小,同理在正四边形A1A2A3A4中,分析可得同样得结论,进而在正n边形A1A2A3…An,类似的分析,可得答案.
解答:图1中,∵弧A1M=弧A2N,
∴∠A1A3M=∠NA1A2,
∴由三角形外角定理可得:∠A3PN=∠A1A3M+A3A1N=∠A3A1A2=60°,为其一个内角;
同理在正四边形A1A2A3A4中,有∠A4PN=∠A1A2A3=90°,为其一个内角;
…,
分析可得:在正n边形A1A2A3…An,亦有∠A4PN=∠A1A2A3,即为其的一个内角;
故∠AnPN=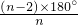 .
.
故答案为:60°,90°,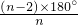 .
.
点评:本题考查了正多边形的概念掌握和计算的能力,注意由特殊到一般的分析思路.

分析:图1中,由三角形外角定理可得∠A3PN的大小等于其一个内角得大小,同理在正四边形A1A2A3A4中,分析可得同样得结论,进而在正n边形A1A2A3…An,类似的分析,可得答案.
解答:图1中,∵弧A1M=弧A2N,
∴∠A1A3M=∠NA1A2,
∴由三角形外角定理可得:∠A3PN=∠A1A3M+A3A1N=∠A3A1A2=60°,为其一个内角;
同理在正四边形A1A2A3A4中,有∠A4PN=∠A1A2A3=90°,为其一个内角;
…,
分析可得:在正n边形A1A2A3…An,亦有∠A4PN=∠A1A2A3,即为其的一个内角;
故∠AnPN=
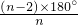 .
.故答案为:60°,90°,
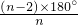 .
.点评:本题考查了正多边形的概念掌握和计算的能力,注意由特殊到一般的分析思路.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
正方形ABCD与正方形CEFG的位置如图所示,点G在线段CD或CD的延长线上,分别连接BD、BF、FD,得到 BFD.
BFD.
(1)在图1、图2、图3中,若正方形CEFG的边长分别为1、3、4,且正方形ABCD的边长均为3,请通过计算填写下表:
图1 图2 图3
| 正方形CEFG的边长 | 1 | 3 | 4 |
 BFD的面积 BFD的面积 | | | |
 ,正方形ABCD的边长为
,正方形ABCD的边长为 ,猜想
,猜想 的大小,并结合图3证明你的猜想.
的大小,并结合图3证明你的猜想.  运动的路程s与运动时间t(秒)之间的函数图象,图3是点P的纵坐标y与点P运动的路程s之间的函数图象的一部分.
运动的路程s与运动时间t(秒)之间的函数图象,图3是点P的纵坐标y与点P运动的路程s之间的函数图象的一部分.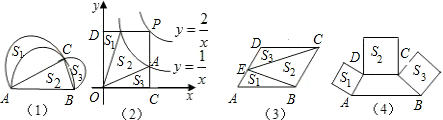
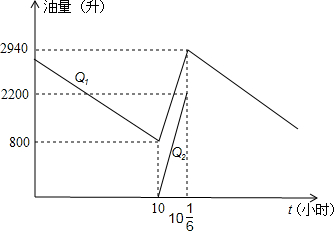 (1)求运输飞机起飞时油箱的油量;
(1)求运输飞机起飞时油箱的油量; 类似地,图2所示的算筹图我们可以表述为( )
类似地,图2所示的算筹图我们可以表述为( )
 B.
B. C.
C. D.
D.