题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点D在
,点D在![]() 上,将
上,将![]() 沿直线
沿直线![]() 翻折后,将点A落在点E处,如果
翻折后,将点A落在点E处,如果![]() ,那么线段
,那么线段![]() 的长为( )
的长为( )

A.![]() B.
B.![]() C.1D.
C.1D.![]()
【答案】B
【解析】
根据翻折变换的性质可得∠ABD=∠EBD,AD=DE,AB=BE,连接AE,可得△ADE是等腰直角三角形,然后求出∠DAE=45°,从而得到∠BAE,再根据等腰三角形两底角相等求出∠ABE,然后求出∠ABD,根据直角三角形两锐角互余求出∠ABC,再求出∠CBD=45°,得到△BCD是等腰直角三角形,根据等腰直角三角形的性质可得CD=BC,然后利用勾股定理列式求出AC,然后根据AD=AC-CD计算得到AD,即为DE的长.
解:∵△ADB沿直线BD翻折后点A落在点E处,
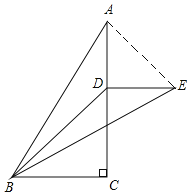
∴∠ABD=∠EBD,AD=DE,AB=BE,
如图,连接AE,
∵DE∥BC,∠C=90°,
∴∠C=![]() ,
,
![]() ∠ADE=90°,
∠ADE=90°,
∴△ADE是等腰直角三角形,
∴∠DAE=45°,
∵∠BAC=30°,
∴∠BAE=30°+45°=75°,
在△ABE中,∠ABE=180°-2×75°=30°,
∴∠ABD=![]() ∠ABE=
∠ABE=![]() ×30°=15°,
×30°=15°,
∵∠BAC=30°,∠C=90°,AB=2,
∴∠ABC=90°-30°=60°,BC=1,
∴∠CBD=∠ABC-∠ABD=60°-15°=45°,
∴△BCD是等腰直角三角形,
∴CD=BC=1,
在Rt△ABC中,AB=2,BC=1,
∴AC=![]()
∴AD=AC-CD=![]() 即DE=
即DE=![]()
故选:B.

练习册系列答案
相关题目






