题目内容
已知:一只木箱放在水平地面上,其截面为矩形ABCD,AB= cm,BC=1cm,一根长为4m的竹竿MN倾斜搁在箱子上,MN与地面所成的锐角为α
cm,BC=1cm,一根长为4m的竹竿MN倾斜搁在箱子上,MN与地面所成的锐角为α
(1)当α由30°增大到45°时,求竹竿顶端N上升的高度.(结果保留根号)
(2)当tanα=______时,点D到MN的距离最大.

解:(1)当α=30°时,竹竿顶端的高度h1= MN=
MN= 4=2(cm),
4=2(cm),
当α=45°时,顶端高度h2=MN•sin45°=4× =2
=2 (cm),
(cm),
则上升高度为:h2-h1=(2 -2)cm.
-2)cm.
(2)当D到MN的距离最大时,就是上升到最大高度,
∵AB= cm,BC=1cm,
cm,BC=1cm,
∴BD= =
= =
= ,
,
∵h=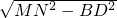 =
= ,
,
∴tanα=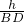 =
= .
.
故答案为: .
.
分析:(1)先求出当α=30°时,竹竿顶端的高度,再求出当α=45°时,顶端高度,即可得出上升高度.
(2)当D到MN的距离最大时,就是上升到最大高度,根据勾股定理求出BD的值,再求出h的值,最后根据tanα=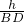 ,即可求出答案.
,即可求出答案.
点评:此题考查了坡度坡角解直角三角形,用到的知识点是坡度坡角的概念、解直角三角形,关键是读懂题意,列出算式.
 MN=
MN= 4=2(cm),
4=2(cm),当α=45°时,顶端高度h2=MN•sin45°=4×
 =2
=2 (cm),
(cm),则上升高度为:h2-h1=(2
 -2)cm.
-2)cm.(2)当D到MN的距离最大时,就是上升到最大高度,
∵AB=
 cm,BC=1cm,
cm,BC=1cm,∴BD=
 =
= =
= ,
,∵h=
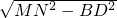 =
= ,
,∴tanα=
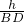 =
= .
.故答案为:
 .
.分析:(1)先求出当α=30°时,竹竿顶端的高度,再求出当α=45°时,顶端高度,即可得出上升高度.
(2)当D到MN的距离最大时,就是上升到最大高度,根据勾股定理求出BD的值,再求出h的值,最后根据tanα=
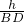 ,即可求出答案.
,即可求出答案.点评:此题考查了坡度坡角解直角三角形,用到的知识点是坡度坡角的概念、解直角三角形,关键是读懂题意,列出算式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
上网费包括网络使用费(每月38元)和上网通信费(每时2元),某电信局对拨号上网用户实行优惠,具体优惠政策如下:
| 上网时间 | 优惠标准 |
| 30小时以内(包括30小时) | 无优惠 |
| 30至50小时之间(包括50小时) | 通信费优惠30% |
| 50至100小时之间(包括100小时) | 通信费优惠40% |
| 100小时以上 | 通信费优惠60% |
(2)若小明家五月份上网80小时,则应缴上网费多少元?
(3)如果用T表示每月的上网时间,M表示上网费,你能用代数式分别表示出各时间段的上网费用吗?
 如图,P是∠AOB平分线上任意一点,PD⊥OA且PD=2cm,若使PE=2cm,则PE与OB的关系是________.
如图,P是∠AOB平分线上任意一点,PD⊥OA且PD=2cm,若使PE=2cm,则PE与OB的关系是________. 的系数是________,次数是________.
的系数是________,次数是________. 电信公司要修建一个服务站,如图所示,按设计要求,服务站到两个城市A,B的距离必须相等,且到两条公路a和b的距离相等.服务站P应修建在什么位置?在图上标出它的位置.
电信公司要修建一个服务站,如图所示,按设计要求,服务站到两个城市A,B的距离必须相等,且到两条公路a和b的距离相等.服务站P应修建在什么位置?在图上标出它的位置.