ΧβΡΩΡΎ»ί
»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§“Μ≈ΉΈοœΏΒΡΕ‘≥Τ÷αΈΣ÷±œΏx=1Θ§”κy÷αΗΚΑκ÷αΫΜ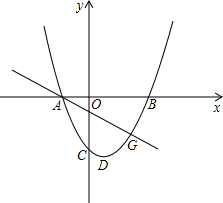 ”ΎCΒψΘ§”κx÷αΫΜ”ΎAΓΔBΝΫΒψΘ§Τδ÷–BΒψΒΡΉχ±ξΈΣΘ®3Θ§0Θ©Θ§CΒψΉχ±ξΈΣΘ®0Θ§-3Θ©Θ°
”ΎCΒψΘ§”κx÷αΫΜ”ΎAΓΔBΝΫΒψΘ§Τδ÷–BΒψΒΡΉχ±ξΈΣΘ®3Θ§0Θ©Θ§CΒψΉχ±ξΈΣΘ®0Θ§-3Θ©Θ°Θ®1Θ©«σ¥Υ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©»τΒψGΘ®2Θ§-3Θ© «ΗΟ≈ΉΈοœΏ…œ“ΜΒψΘ§ΒψE «÷±œΏAGœ¬ΖΫΒΡ≈ΉΈοœΏ…œ“ΜΕ·ΒψΘ§Β±ΒψE‘ΥΕ·ΒΫ ≤Ο¥ΈΜ÷Ο ±Θ§ΓςAEGΒΡΟφΜΐΉν¥σΘΩ«σ≥ω¥Υ ±EΒψΒΡΉχ±ξΚΆΓςAEGΒΡΉν¥σΟφΜΐΘΜ
Θ®3Θ©»τΤΫ––”Ύx÷αΒΡ÷±œΏ”κΗΟ≈ΉΈοœΏΫΜ”ΎMΓΔNΝΫΒψΘ®Τδ÷–ΒψM‘ΎΒψNΒΡ”“≤ύΘ©Θ§‘Ύx÷α…œ «Ζώ¥φ‘ΎΒψQΘ§ ΙΓςMNQΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ωΒψQΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
Ζ÷ΈωΘΚΘ®1Θ©ΗυΨί≈ΉΈοœΏΒΡΕ‘≥Τ÷αΖΫ≥ΧΦΑBΒψΉχ±ξΘ§Ω…«σΒΟAΒψΉχ±ξΘ§‘Ό”Ο¥ΐΕ®œΒ ΐΖ®«σ≥ω≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©Ω…Ζ÷±πΙΐEΓΔGΉςx÷αΒΡ¥ΙœΏΘ§…η¥ΙΉψΈΣFΓΔHΘΜΡ«Ο¥ΓςAGEΒΡΟφΜΐ=ΓςAEFΒΡΟφΜΐ+ΥΡ±Ώ–ΈFHGEΒΡΟφΜΐ-ΓςAGHΒΡΟφΜΐΘ§…η≥ωEΒψΒΡΉχ±ξΘ§Φ¥Ω…±μ Ψ≥ωFΒψΉχ±ξΦΑEFΒΡ≥ΛΘ§ΗυΨί…œΟφΥυΒΟ≥ωΒΡΟφΜΐΦΤΥψΖΫΖ®Θ§Ω…ΒΟ≥ωΙΊ”ΎΓςAGEΒΡΟφΜΐ”κEΒψΚαΉχ±ξΒΡΚ· ΐΙΊœΒ ΫΘ§ΗυΨίΥυΒΟΚ· ΐΒΡ–‘÷ Θ§Φ¥Ω…«σ≥ωΓςAGEΒΡΉν¥σΟφΜΐΦΑΕ‘”ΠΒΡEΒψΉχ±ξΘΜ
Θ®3Θ©Ζ÷ΝΫ÷÷«ιΩωΧ÷¬έΘΚ
ΔΌ“‘MNΈΣ–±±ΏΘ§‘ρQΒψ‘ΎMNΒΡ¥Ι÷±ΤΫΖ÷œΏ…œΘ§Φ¥QΒψΈΣ≈ΉΈοœΏΕ‘≥Τ÷α”κx÷αΫΜΒψΘ§”…¥ΥΩ…ΒΟ≥ωQΒψΉχ±ξΘΜ
ΔΎ“‘MNΈΣ÷±Ϋ«±ΏΘΜ…η≥ωMΓΔNΒΡΉχ±ξΘ§Ω…±μ Ψ≥ωMNΒΡ≥ΛΘ§”…”ΎΓςMNQ «Β»―ϋRtΓςΘ§‘ρMNΒΡ≥Λ”κMΓΔNΒΡΉίΉχ±ξΒΡΨχΕ‘÷ΒœύΆ§Θ§”…¥ΥΩ…«σ≥ωMΓΔNΒΡΉχ±ξΘ§“≤ΨΆ«σ≥ωΝΥQΒψΒΡΉχ±ξΘ°
Θ®2Θ©Ω…Ζ÷±πΙΐEΓΔGΉςx÷αΒΡ¥ΙœΏΘ§…η¥ΙΉψΈΣFΓΔHΘΜΡ«Ο¥ΓςAGEΒΡΟφΜΐ=ΓςAEFΒΡΟφΜΐ+ΥΡ±Ώ–ΈFHGEΒΡΟφΜΐ-ΓςAGHΒΡΟφΜΐΘ§…η≥ωEΒψΒΡΉχ±ξΘ§Φ¥Ω…±μ Ψ≥ωFΒψΉχ±ξΦΑEFΒΡ≥ΛΘ§ΗυΨί…œΟφΥυΒΟ≥ωΒΡΟφΜΐΦΤΥψΖΫΖ®Θ§Ω…ΒΟ≥ωΙΊ”ΎΓςAGEΒΡΟφΜΐ”κEΒψΚαΉχ±ξΒΡΚ· ΐΙΊœΒ ΫΘ§ΗυΨίΥυΒΟΚ· ΐΒΡ–‘÷ Θ§Φ¥Ω…«σ≥ωΓςAGEΒΡΉν¥σΟφΜΐΦΑΕ‘”ΠΒΡEΒψΉχ±ξΘΜ
Θ®3Θ©Ζ÷ΝΫ÷÷«ιΩωΧ÷¬έΘΚ
ΔΌ“‘MNΈΣ–±±ΏΘ§‘ρQΒψ‘ΎMNΒΡ¥Ι÷±ΤΫΖ÷œΏ…œΘ§Φ¥QΒψΈΣ≈ΉΈοœΏΕ‘≥Τ÷α”κx÷αΫΜΒψΘ§”…¥ΥΩ…ΒΟ≥ωQΒψΉχ±ξΘΜ
ΔΎ“‘MNΈΣ÷±Ϋ«±ΏΘΜ…η≥ωMΓΔNΒΡΉχ±ξΘ§Ω…±μ Ψ≥ωMNΒΡ≥ΛΘ§”…”ΎΓςMNQ «Β»―ϋRtΓςΘ§‘ρMNΒΡ≥Λ”κMΓΔNΒΡΉίΉχ±ξΒΡΨχΕ‘÷ΒœύΆ§Θ§”…¥ΥΩ…«σ≥ωMΓΔNΒΡΉχ±ξΘ§“≤ΨΆ«σ≥ωΝΥQΒψΒΡΉχ±ξΘ°
Ϋβ¥πΘΚΫβΘΚΘ®1Θ©ΓΏ≈ΉΈοœΏΒΡΕ‘≥Τ÷αΈΣx=1Θ§«“BΘ®3Θ§0Θ©Θ§
ΓύAΘ®-1Θ§0Θ©ΘΜ
Ω……η≈ΉΈοœΏΒΡΫβΈω ΫΈΣΘΚy=aΘ®x-3Θ©Θ®x+1Θ©Θ§‘ρ”–ΘΚ
Θ®-3Θ©ΓΝ1ΓΝa=-3Θ§a=1ΘΜ
Γύy=x2-2x-3Θ®4Ζ÷Θ©
Θ®2Θ©Β±E‘ΥΕ·ΒΫ(
Θ§-
) ±”–Ήν¥σΟφΜΐΘ§Ήν¥σΟφΜΐ «
Θ§άμ”…»γœ¬ΘΚ
ΙΐEΉςEFΓΆx÷α”ΎFΘ§ΙΐGΉςGHΓΆx÷α”ΎHΘΜ
…ηEΘ®x0Θ§y0Θ©Θ§‘ρFΘ®x0Θ§0Θ©Θ§EF=-Θ®x02-2x0-3Θ©
“ρΈΣGΘ®2Θ§-3Θ©Υυ“‘GH=3
SΓςAEF=
y0Θ§SΓςAGH=
=
SΥΡ±Ώ–ΈFHGE=
=
Υυ“‘SΓςAGE=SΓςAEF+SΥΡ±Ώ–ΈFHGE-SΓςAGH=-
x02+
x0+3=-
(x0-
)2+
Θ®6Ζ÷Θ©
Β±x0=
±Θ§”–Ήν¥σ÷ΒΈΣ
ΘΜΘ®7Ζ÷
ΫΪx0=
¥ζ»κy=x2-2x-3Θ§
ΒΟy0=-
ΘΜ
Υυ“‘E(
Θ§-
)ΘΜΘ®8Ζ÷Θ©
Θ®3Θ©¥φ‘ΎΘ§QΘ®1Θ§0Θ©ΜρΘ®Γά
Θ§0Θ©ΜρΘ®2Γά
Θ§0Θ©άμ”…»γœ¬Θ®9Ζ÷Θ©
“ρΈΣMNΤΫ––”κx÷αΘ§
Υυ“‘MΓΔNΙΊ”Ύx=1Ε‘≥Τ
ΔΌ»τNQ=QMΘ§‘ρQ±Ί‘ΎMNΒΡ÷–¥ΙœΏΦ¥Ε‘≥Τ÷αx=1…œΘ§Υυ“‘QΘ®1Θ§0Θ©Θ®10Ζ÷Θ©
ΔΎ»τQN=MNΘ§‘ρΓœQMN=90ΓψΘ§…ηMΘ®m1Θ§n1Θ©
 ‘ρ”–ΘΚNΘ®2-m1Θ§n1Θ©Θ§MN=m1-Θ®2-m1Θ©=2m1-2
‘ρ”–ΘΚNΘ®2-m1Θ§n1Θ©Θ§MN=m1-Θ®2-m1Θ©=2m1-2
QN=|n1|Θ§
Υυ“‘|n1|=2m1-2Θ§Τδ÷–n1=m12-2m1-3
Ά§άμ»τQM=MNΘ§QM=|n1|Θ§n1=m12-2m1-3Θ§
Ήέ…œΩ…ΒΟ|n1|=2m1-2
ΫβΒΟm1=
Μρ-
Μρ2+
Μρ2-
ΘΜΘ®12Ζ÷Θ©
ΓύQ1Θ®
Θ§0Θ©Θ§Q2Θ®-
Θ§0Θ©Θ§Q3Θ®2+
Θ§0Θ©Θ§Q4Θ®2-
Θ§0Θ©Θ°
Ήέ…œΥυ ωΘ§¥φ‘ΎΖϊΚœΧθΦΰΒΡQΒψΘ§
«“Ήχ±ξΈΣΘΚQ1Θ®
Θ§0Θ©Θ§Q2Θ®-
Θ§0Θ©Θ§Q3Θ®2+
Θ§0Θ©Θ§Q4Θ®2-
Θ§0Θ©Θ§Q5Θ®1Θ§0Θ©Θ°
ΓύAΘ®-1Θ§0Θ©ΘΜ
Ω……η≈ΉΈοœΏΒΡΫβΈω ΫΈΣΘΚy=aΘ®x-3Θ©Θ®x+1Θ©Θ§‘ρ”–ΘΚ
Θ®-3Θ©ΓΝ1ΓΝa=-3Θ§a=1ΘΜ

Γύy=x2-2x-3Θ®4Ζ÷Θ©
Θ®2Θ©Β±E‘ΥΕ·ΒΫ(
| 1 |
| 2 |
| 15 |
| 4 |
| 27 |
| 8 |
ΙΐEΉςEFΓΆx÷α”ΎFΘ§ΙΐGΉςGHΓΆx÷α”ΎHΘΜ
…ηEΘ®x0Θ§y0Θ©Θ§‘ρFΘ®x0Θ§0Θ©Θ§EF=-Θ®x02-2x0-3Θ©
“ρΈΣGΘ®2Θ§-3Θ©Υυ“‘GH=3
SΓςAEF=
| -(x0+1) |
| 2 |
| AM•MH |
| 2 |
| 9 |
| 2 |
SΥΡ±Ώ–ΈFHGE=
| (MH+EF)HF |
| 2 |
| x0y0-3x0-2y0+6 |
| 2 |
Υυ“‘SΓςAGE=SΓςAEF+SΥΡ±Ώ–ΈFHGE-SΓςAGH=-
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 27 |
| 8 |
Β±x0=
| 1 |
| 2 |
| 27 |
| 8 |
ΫΪx0=
| 1 |
| 2 |

ΒΟy0=-
| 15 |
| 4 |
Υυ“‘E(
| 1 |
| 2 |
| 15 |
| 4 |
Θ®3Θ©¥φ‘ΎΘ§QΘ®1Θ§0Θ©ΜρΘ®Γά
| 5 |
| 5 |
“ρΈΣMNΤΫ––”κx÷αΘ§
Υυ“‘MΓΔNΙΊ”Ύx=1Ε‘≥Τ
ΔΌ»τNQ=QMΘ§‘ρQ±Ί‘ΎMNΒΡ÷–¥ΙœΏΦ¥Ε‘≥Τ÷αx=1…œΘ§Υυ“‘QΘ®1Θ§0Θ©Θ®10Ζ÷Θ©
ΔΎ»τQN=MNΘ§‘ρΓœQMN=90ΓψΘ§…ηMΘ®m1Θ§n1Θ©
 ‘ρ”–ΘΚNΘ®2-m1Θ§n1Θ©Θ§MN=m1-Θ®2-m1Θ©=2m1-2
‘ρ”–ΘΚNΘ®2-m1Θ§n1Θ©Θ§MN=m1-Θ®2-m1Θ©=2m1-2QN=|n1|Θ§
Υυ“‘|n1|=2m1-2Θ§Τδ÷–n1=m12-2m1-3
Ά§άμ»τQM=MNΘ§QM=|n1|Θ§n1=m12-2m1-3Θ§
Ήέ…œΩ…ΒΟ|n1|=2m1-2
ΫβΒΟm1=
| 5 |
| 5 |
| 5 |
| 5 |
ΓύQ1Θ®
| 5 |
| 5 |
| 5 |
| 5 |
Ήέ…œΥυ ωΘ§¥φ‘ΎΖϊΚœΧθΦΰΒΡQΒψΘ§
«“Ήχ±ξΈΣΘΚQ1Θ®
| 5 |
| 5 |
| 5 |
| 5 |
ΒψΤάΘΚ¥ΥΧβΩΦ≤ιΝΥΕΰ¥ΈΚ· ΐΫβΈω ΫΒΡ»ΖΕ®ΓΔΆΦ–ΈΟφΜΐΒΡ«σΖ®ΓΔΕΰ¥ΈΚ· ΐΒΡ”Π”ΟΓΔΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΒΡ≈–Ε®ΚΆ–‘÷ Β»÷Σ ΕΘ§ΉέΚœ–‘«ΩΘ§ΡήΝΠ“Σ«σΫœΗΏΘ°ΩΦ≤ι―ß…ζΖ÷άύΧ÷¬έΘ§ ΐ–ΈΫαΚœΒΡ ΐ―ßΥΦœκΖΫΖ®Θ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
 ΩΤ―ß Β―ιΜνΕ·≤αœΒΝ–¥πΑΗ
ΩΤ―ß Β―ιΜνΕ·≤αœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ
 »γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξ÷–Θ§ΥΡ±Ώ–ΈOABC «Β»―ϋΧί–ΈΘ§CBΓΈOAΘ§OA=7Θ§AB=4Θ§ΓœCOA=60ΓψΘ§ΒψPΈΣx÷α…œΒΡ“ΜΗωΕ·ΒψΘ§ΒΪ «ΒψP≤Μ”κΒψ0ΓΔΒψA÷ΊΚœΘ°Ν§Ϋ”CPΘ§DΒψ «œΏΕΈAB…œ“ΜΒψΘ§Ν§Ϋ”PDΘ°
»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξ÷–Θ§ΥΡ±Ώ–ΈOABC «Β»―ϋΧί–ΈΘ§CBΓΈOAΘ§OA=7Θ§AB=4Θ§ΓœCOA=60ΓψΘ§ΒψPΈΣx÷α…œΒΡ“ΜΗωΕ·ΒψΘ§ΒΪ «ΒψP≤Μ”κΒψ0ΓΔΒψA÷ΊΚœΘ°Ν§Ϋ”CPΘ§DΒψ «œΏΕΈAB…œ“ΜΒψΘ§Ν§Ϋ”PDΘ° Θ®2012•”ε±±«χ“ΜΡΘΘ©»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξxoy÷–Θ§“‘Ήχ±ξ‘≠ΒψOΈΣ‘≤–ΡΘ§3ΈΣΑκΨΕΜ≠‘≤Θ§¥”¥Υ‘≤ΡΎΘ®Αϋά®±ΏΫγΘ©ΒΡΥυ”–’ϊ ΐΒψΘ®ΚαΓΔΉίΉχ±ξΨυΈΣ’ϊ ΐΘ©÷–»Έ“β―ûÓΜΗωΒψΘ§ΤδΚαΓΔΉίΉχ±ξ÷°ΚΆΈΣ0ΒΡΗ≈¬ «
Θ®2012•”ε±±«χ“ΜΡΘΘ©»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξxoy÷–Θ§“‘Ήχ±ξ‘≠ΒψOΈΣ‘≤–ΡΘ§3ΈΣΑκΨΕΜ≠‘≤Θ§¥”¥Υ‘≤ΡΎΘ®Αϋά®±ΏΫγΘ©ΒΡΥυ”–’ϊ ΐΒψΘ®ΚαΓΔΉίΉχ±ξΨυΈΣ’ϊ ΐΘ©÷–»Έ“β―ûÓΜΗωΒψΘ§ΤδΚαΓΔΉίΉχ±ξ÷°ΚΆΈΣ0ΒΡΗ≈¬ « »γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξ÷–Θ§Β»―ϋΧί–ΈABCDΒΡœ¬ΒΉ‘Ύx÷α…œΘ§«“BΒψΉχ±ξΈΣΘ®4Θ§0Θ©Θ§DΒψΉχ±ξΈΣΘ®0Θ§3Θ©Θ§‘ρAC≥ΛΈΣ
»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξ÷–Θ§Β»―ϋΧί–ΈABCDΒΡœ¬ΒΉ‘Ύx÷α…œΘ§«“BΒψΉχ±ξΈΣΘ®4Θ§0Θ©Θ§DΒψΉχ±ξΈΣΘ®0Θ§3Θ©Θ§‘ρAC≥ΛΈΣ »γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξxOy÷–Θ§“―÷ΣΒψAΘ®-5Θ§0Θ©Θ§P «Ζ¥±»άΐΚ· ΐ
»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξxOy÷–Θ§“―÷ΣΒψAΘ®-5Θ§0Θ©Θ§P «Ζ¥±»άΐΚ· ΐ ΓœCOA=45ΓψΘ§Ε·ΒψP¥”ΒψO≥ωΖΔΘ§‘ΎΧί–ΈOABCΒΡ±Ώ…œ‘ΥΕ·Θ§¬ΖΨΕΈΣOΓζAΓζBΓζCΘ§ΒΫ¥οΒψC ±ΆΘ÷ΙΘ°Ής÷±œΏCPΘ°
ΓœCOA=45ΓψΘ§Ε·ΒψP¥”ΒψO≥ωΖΔΘ§‘ΎΧί–ΈOABCΒΡ±Ώ…œ‘ΥΕ·Θ§¬ΖΨΕΈΣOΓζAΓζBΓζCΘ§ΒΫ¥οΒψC ±ΆΘ÷ΙΘ°Ής÷±œΏCPΘ°