题目内容
15.怎样用一条长40cm的绳子围成一个面积为96cm2的矩形?能围成一个面积为102cm2的矩形吗?如果能,说明围法;如果不能,说明理由.分析 首先设矩形的长为xcm,则宽为(20-x)cm,再利用矩形面积公式列出方程x(20-x)=96或x(20-x)=102,得出根据根的判别式的符号,进而得出答案.
解答 解:设所围矩形的长为xcm,则所围矩形的宽为(20-x)cm,
(1)依题意,得 x(20-x)=96,
化简,得 x2-20x+96=0.
解,得 x1=8,x2=12.
当x=8时,20-x=12;
当x=12时,20-x=8.
所以,当所围矩形的长为12cm,宽为8cm时,它的面积为96cm2.
(2)依题意,得 x(20-x)=102
化简,得 x2-20x+102=0.
∵△=b2-4ac=(-20)2-4×102=400-408=-8<0,
∴方程无实数根.
所以用一条长40cm的绳子不能围成一个面积为102cm2的矩形.
点评 此题主要考查了一元二次方程的应用,熟练应用根的判别式是解题关键.

练习册系列答案
相关题目
3.下列计算正确的是( )
| A. | (x3)3=x9 | B. | (-2x)3=-6x3 | C. | 2x2-x=x | D. | x2÷x3=x2 |
10.0.5的倒数为( )
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
20.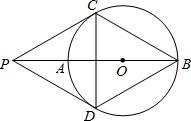 如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙O上一点,连接PD.已知PC=PD=BC.下列结论:(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=CD;(4)弧AC=弧AD.其中正确的个数为( )
如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙O上一点,连接PD.已知PC=PD=BC.下列结论:(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=CD;(4)弧AC=弧AD.其中正确的个数为( )
 如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙O上一点,连接PD.已知PC=PD=BC.下列结论:(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=CD;(4)弧AC=弧AD.其中正确的个数为( )
如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙O上一点,连接PD.已知PC=PD=BC.下列结论:(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=CD;(4)弧AC=弧AD.其中正确的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.若一次函数y=2mx+(m2-2m)的图象经过坐标原点,则( )
| A. | m=0或m=2 | B. | m=0 | C. | m=2 | D. | 无法确定 |
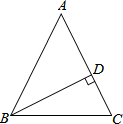 已知:如图,△ABC中,AB=AC,BD是AC边上的高
已知:如图,△ABC中,AB=AC,BD是AC边上的高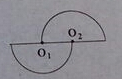 如图,⊙O1、⊙O2分别是两个半圆的圆心,这个圆形是中心对称图形吗?如果是,请指出对称中心;如果不是,请说明理由.
如图,⊙O1、⊙O2分别是两个半圆的圆心,这个圆形是中心对称图形吗?如果是,请指出对称中心;如果不是,请说明理由.