题目内容
已知,如图8 ,正方形ABCD边长是4,P是CD的中点,Q是线段BC上异于B的一点,当BQ = 时,△ADP与△PCQ相似.

8
答案为:3
若要使ADP与△PCQ相似,有条件可知AD和CP是对应边,DP和CQ是对应边,利用比例式 可求出CQ的值,BC已知,进而求出BQ的值.
可求出CQ的值,BC已知,进而求出BQ的值.
证明:∵正方形ABCD边长是4,P是CD的中点,
∴DP=PC=2.
∵△ADP∽△PCQ,
∴ ,
,
∴ ,
,
∴CQ=1,
∴BQ=4-1=3.
即当BQ=3 时,△ADP与△PCQ相似.
故答案为:3.
若要使ADP与△PCQ相似,有条件可知AD和CP是对应边,DP和CQ是对应边,利用比例式
 可求出CQ的值,BC已知,进而求出BQ的值.
可求出CQ的值,BC已知,进而求出BQ的值.证明:∵正方形ABCD边长是4,P是CD的中点,
∴DP=PC=2.
∵△ADP∽△PCQ,
∴
 ,
,∴
 ,
,∴CQ=1,
∴BQ=4-1=3.
即当BQ=3 时,△ADP与△PCQ相似.
故答案为:3.

练习册系列答案
相关题目
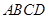 的顶点
的顶点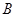 作直线
作直线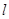 ,过
,过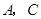 作
作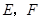 .若
.若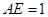 ,
,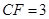 ,则
,则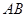 的长度为 .
的长度为 .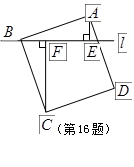


 的值;
的值; ,请用
,请用 来表示
来表示
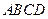 的对角线
的对角线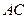 和
和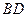 相交于点
相交于点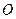 ,
,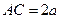 ,
,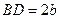 ,
,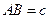
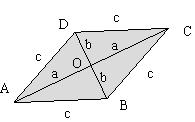
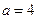 ,
,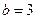 ,求
,求 中,
中,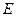 是
是 边上一点,
边上一点, 为
为 延长线上的点,
延长线上的点, .
.
 ≌△
≌△
 ,求
,求 的度数
的度数