题目内容
半径相等的圆的内接正三角形和正方形,正三角形与正方形的边长之比为
- A.1:

- B.
 :
:
- C.3:2
- D.1:2
B
分析:可以构造一个由正多边形的半径、边心距和半边组成的直角三角形来解决问题.
解答:设其半径是R,则其正三角形的边长是 R,
R,
正方形的边长是 R,则它们的比是
R,则它们的比是 :
: .故选B.
.故选B.
点评:能够构造一个由正多边形的半径、边心距和半边组成的直角三角形.该正多边形的半径即是圆的半径,其半边所对的角是它的中心角的一半,即 .
.
分析:可以构造一个由正多边形的半径、边心距和半边组成的直角三角形来解决问题.
解答:设其半径是R,则其正三角形的边长是
 R,
R,正方形的边长是
 R,则它们的比是
R,则它们的比是 :
: .故选B.
.故选B.点评:能够构造一个由正多边形的半径、边心距和半边组成的直角三角形.该正多边形的半径即是圆的半径,其半边所对的角是它的中心角的一半,即
 .
. 
练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案
相关题目
半径相等的圆的内接正三角形、正方形、正六边形的边长之比为( )
A、1:
| ||||
B、
| ||||
| C、3:2:1 | ||||
| D、1:2:3 |
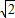 :
: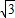
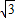 :
: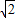 :1
:1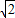 :
: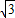
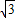 :
: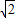 :1
:1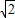 :
: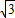
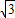 :
: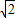 :1
:1