题目内容
半径相等的圆的内接正三角形、正方形、正六边形的边长之比为( )
A、1:
| ||||
B、
| ||||
| C、3:2:1 | ||||
| D、1:2:3 |
分析:从中心向边作垂线,构建直角三角形,通过解直角三角形可得.
解答:解:设圆的半径是r,
则多边形的半径是r,
则内接正三角形的边长是2rsin60°=
r,
内接正方形的边长是2rsin45°=
r,
正六边形的边长是r,
因而半径相等的圆的内接正三角形、正方形、正六边形的边长之比为
:
:1.
故选B.
则多边形的半径是r,
则内接正三角形的边长是2rsin60°=
| 3 |
内接正方形的边长是2rsin45°=
| 2 |
正六边形的边长是r,
因而半径相等的圆的内接正三角形、正方形、正六边形的边长之比为
| 3 |
| 2 |
故选B.
点评:正多边形的计算一般是通过中心作边的垂线,连接半径,把正多边形中的半径,边长,边心距,中心角之间的计算转化为解直角三角形.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
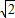 :
: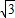
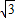 :
: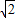 :1
:1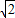 :
: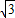
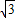 :
: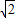 :1
:1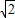 :
: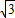
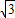 :
: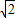 :1
:1