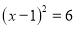题目内容
式子(-5a2+4b2)( )=25a4-16b4中括号内应填( )
A. 5a2+4b2 B. 5a2-4b2 C. -5a2+4b2 D. -5a2-4b2
【答案】D
【解析】解析:∵(-5a2+4b2)(-5a2-4b2)=25a4-16b4,
∴括号内应填-5a2-4b2.故选D.
【题型】单选题
【结束】
7
下列等式成立的是( )
A. (-a-b)2+(a-b)2=-4ab B. (-a-b)2+(a-b)2=a2+b2
C. (-a-b)(a-b)=(a-b)2 D. (-a-b)(a-b)=b2-a2
D 【解析】解析:∵(-a-b)2+(a-b)2=(a+b)2+(a-b)2=(a2+2ab+b2)+(a2-2ab+b2)=2a2+2b2, ∴选项A与选项B错误; ∵(-a-b)(a-b)=-(a+b)(a-b)=-(a2-b2)=b2-a2,∴选项C错误,选项D正确. 故选D.
练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目


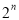
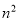
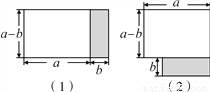
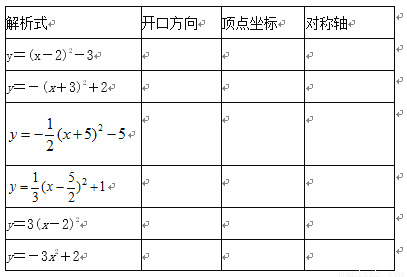
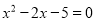 时,原方程应变形为
时,原方程应变形为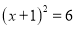 B.
B. 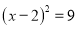 C.
C. 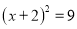 D.
D.