题目内容
【题目】在![]() 中,
中,![]() ,
,![]() 为斜边
为斜边![]() 上的中线;在
上的中线;在![]() 中,
中,![]() ,
,![]() ,且
,且![]() .连接
.连接![]() ,点
,点![]() 、点
、点![]() 分别为线段
分别为线段![]() 的中点,连接
的中点,连接![]() .
.
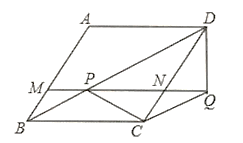
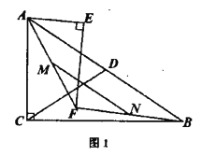
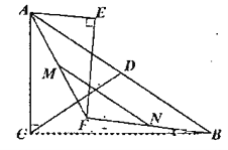
![]() 如图1,当点
如图1,当点![]() 在
在![]() 内部时,求证:
内部时,求证:![]()
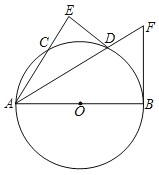
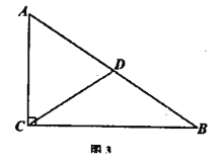
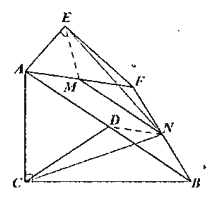
![]() 如图2,当点
如图2,当点![]() 在
在![]() 外部时,连接
外部时,连接![]() ,判断
,判断![]() 与
与![]() 的数量关系,并加以证明;
的数量关系,并加以证明;

![]() 将图1中的
将图1中的![]() 绕点
绕点![]() 旋转,在旋转的过程中,请直接回答:
旋转,在旋转的过程中,请直接回答:
①![]() 中的
中的![]() 与
与![]() 的数量关系是否发生了变化?
的数量关系是否发生了变化?
②若![]() ,当点
,当点![]() 三点在同一条直线上时,请直搂写出
三点在同一条直线上时,请直搂写出![]() 的值.
的值.
【答案】(1)见解析;(2)![]() ;(3)①
;(3)①![]() 与
与![]() 的数量关系不变
的数量关系不变![]() ;②
;②![]() 或
或![]()
【解析】
(1)利用直角三角形的斜边的中线等于斜边的一半和三角形的中位线即可;
(2)根据三角形的中位线和直角三角形斜边上的中线等于斜边的一半可知:![]() 由等边对等角可知
由等边对等角可知![]() 再由平行线的性质可知
再由平行线的性质可知![]() 因此得出:
因此得出:![]() ,所以证得△EMN≌△DNC进而得出结论;
,所以证得△EMN≌△DNC进而得出结论;
(3)①借助(2)得出结论;
②分两种情况,如图,先判断出点N是以点D为圆心,![]() 为半径的圆上,即可得出结论.
为半径的圆上,即可得出结论.
(1)证明,在![]() 中
中
![]() 是斜边
是斜边![]() 上的中线
上的中线
![]()
在![]() 中,
中,![]() 点
点![]() 分别是边
分别是边![]() 的中点,
的中点,
![]()
![]()
(2)CN与![]() 的数量关系是
的数量关系是![]()
证明:如图,连接![]() 。
。
在![]() 中,
中,![]() 是斜边
是斜边![]() 上的中线,
上的中线,![]()
![]()
在![]() 中,点
中,点![]() 是斜边
是斜边![]() 的中点,
的中点,
![]()
![]()
![]()
![]()
![]()
![]() 中,点
中,点![]() 、点
、点![]() 、点
、点![]() 分别为线段
分别为线段![]() 的中点,
的中点,
![]() ,
,
![]()
![]()
![]()
![]()
![]()
即![]()
![]()
![]()
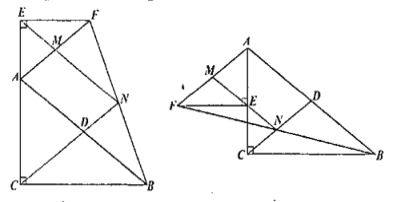
(3)①![]() 与
与![]() 的数量关系不变
的数量关系不变![]()
与(2)同理可证;
②![]() 或
或![]()
分两种情况,如图,
由(2)可知:点N在以点D 为圆心,![]() 为半径的圆上,
为半径的圆上,
在Rt△ABC中,CD是AB边上的中线,
∴CD=![]() AB=
AB=![]() a
a
∵点D、N分别是AB、BF的中点,
∴DN=![]() AF=
AF=![]() b
b
∴CN最大=CD+DN=![]() ,CN最小=CD-DN=
,CN最小=CD-DN=![]()
由(2)可知:EN=CN
∴EN最大=![]() ,EN最小=
,EN最小=![]()
∴EN的最大值为![]() ,EN的最小值为
,EN的最小值为![]()
∴EN的值为![]() 或者
或者![]()

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目