题目内容
7．已知抛物线y=a（x-m+5）2+2n与y=a（x+n-1）2+12关于y轴对称，试求m，n的值．分析 根据两个二次函数关于y轴对称，可得它们的顶点坐标关于y轴对称，根据关于y轴对称的点的横坐标互为相反数，纵坐标相等，可得方程组，根据解方程组，可得答案．
解答 解：由y=a（x-m+5）2+2n与y=a（x+n-1）2+12关于y轴对称，得
$\left\{\begin{array}{l}{m-5+1-n=0}\\{2n=12}\end{array}\right.$．
解得$\left\{\begin{array}{l}{m=10}\\{n=6}\end{array}\right.$．
故m的值为10，n的值为6．
点评 本题考查了二次函数图象与几何变换，利用两个二次函数关于y轴对称得出它们的顶点坐标关于y轴对称是解题关键，注意关于y轴对称的点的横坐标互为相反数，纵坐标相等．
练习册系列答案
相关题目
如图，点A、0、E在同一直线上，OD平分∠COE，OB平分∠AOC，若∠DOE=20°，求∠BOD的度数．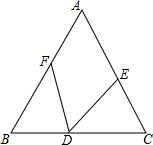
如图，在△ABC中，已知AB=AC，D为BC上一点，BF=CD，CE=BD，求证：∠EDF=90°-$\frac{1}{2}$∠A．