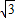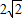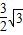题目内容
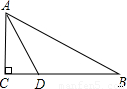
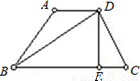
(2002•荆州)如图,一次函数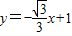 的图象与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等边△ABC,
的图象与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等边△ABC,(1)求△ABC的面积;
(2)如果在第二象限内有一点P(a,
 );试用含有a的代数式表示四边形ABPO的面积,并求出当△ABP的面积与△ABC的面积相等时a的值;
);试用含有a的代数式表示四边形ABPO的面积,并求出当△ABP的面积与△ABC的面积相等时a的值;(3)在x轴上,是否存在点M,使△MAB为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.

【答案】分析:本题首先令x=0,y=0求出一次函数的解析式.然后根据勾股定理求出AB的长,继而可求出三角形ABC的面积.然后依题意可得出S四边形AOBC=S△ACB+S△ACP,当S△ABP=S△ABC时求出a值.
解答:解:(1)分别令y=0和x=0,得一次函数y= x+1的图象与x轴.
x+1的图象与x轴.
y轴的交点坐标分别是A( ,0),B(0,1),即OA=
,0),B(0,1),即OA= ,OB=1,
,OB=1,
∴AB= =2
=2
∵△ABC为等边三角形,
∴S△ABC= ;
;
(2)如图1,S△AOB= ,S△AOP=
,S△AOP= ,S△BOP=
,S△BOP= |a|•OB=-
|a|•OB=- .
.
∴S四边形ABPO=S△AOB+S△BOP= ,
,
而S△ABP=S四边形ABPO-S△APO,
∴当S△ABP=S△ABC时, =
= ,
,
解得a=-
 ;
;

(3)如图2,
满足条件的点M有4个:M1(- ,0),M2(
,0),M2( -2,0),M3(
-2,0),M3( ,0),M4(
,0),M4( +2,0).
+2,0).
点评:本题考查的是一次函数的综合运用以及三角形的面积计算,重点考查考生理解图形的能力.
解答:解:(1)分别令y=0和x=0,得一次函数y=
 x+1的图象与x轴.
x+1的图象与x轴.y轴的交点坐标分别是A(
 ,0),B(0,1),即OA=
,0),B(0,1),即OA= ,OB=1,
,OB=1,∴AB=
 =2
=2∵△ABC为等边三角形,
∴S△ABC=
 ;
;(2)如图1,S△AOB=
 ,S△AOP=
,S△AOP= ,S△BOP=
,S△BOP= |a|•OB=-
|a|•OB=- .
.∴S四边形ABPO=S△AOB+S△BOP=
 ,
,而S△ABP=S四边形ABPO-S△APO,
∴当S△ABP=S△ABC时,
 =
= ,
,解得a=-

 ;
;
(3)如图2,
满足条件的点M有4个:M1(-
 ,0),M2(
,0),M2( -2,0),M3(
-2,0),M3( ,0),M4(
,0),M4( +2,0).
+2,0).点评:本题考查的是一次函数的综合运用以及三角形的面积计算,重点考查考生理解图形的能力.

练习册系列答案
相关题目
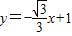 的图象与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等边△ABC,
的图象与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等边△ABC, );试用含有a的代数式表示四边形ABPO的面积,并求出当△ABP的面积与△ABC的面积相等时a的值;
);试用含有a的代数式表示四边形ABPO的面积,并求出当△ABP的面积与△ABC的面积相等时a的值;

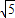
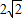
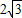 ,则AC的长是( )
,则AC的长是( )