题目内容
一个正多边形所有的对角线的条数与边数的比为9:2,求这个正多边形的一个外角的度数.
考点:多边形的对角线,多边形内角与外角
专题:
分析:n边形对角线的总条数为:
n(n-3)(n≥3,且n为整数),依此根据一个正多边形所有的对角线的条数与边数的比为9:2,列出方程求出这个正多边形的边数,再用360°除以这个正多边形的边数,即可求出这个正多边形的一个外角的度数.
| 1 |
| 2 |
解答:解:依题意有
n(n-3):n=9:2,
解得n=12,
360°÷12=30°.
故这个正多边形的一个外角的度数是30°.
| 1 |
| 2 |
解得n=12,
360°÷12=30°.
故这个正多边形的一个外角的度数是30°.
点评:主要考查了多边形的对角线、多边形外角和、正多边形的性质,关键是掌握正多边形的各个外角相等.

练习册系列答案
相关题目
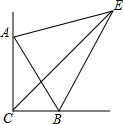 如图,在Rt△ABC中,∠C=90°,∠A=40°,∠C的平分线与∠ABC相邻的外角平分线交于E点,连接AE,则∠AEB等于( )
如图,在Rt△ABC中,∠C=90°,∠A=40°,∠C的平分线与∠ABC相邻的外角平分线交于E点,连接AE,则∠AEB等于( )| A、50° | B、45° |
| C、40° | D、35° |