题目内容
 如图,直线y=kx+b与x轴、y轴交于A、B两点,与双曲线y=
如图,直线y=kx+b与x轴、y轴交于A、B两点,与双曲线y=| 10 | x |
分析:首先作辅助线:过点C作CD⊥AO于D,连接OC,可得△AOB∽△ADC,根据相似三角形的对应边成比例,即可得AD=3AO,然后由点C在双曲线y=
,求得△OCD的面积,则由同高三角形的面积比等于对应底的比求得△ACD的面积,则问题得解.
| 10 |
| x |
解答: 解:过点C作CD⊥AO于D,连接OC,
解:过点C作CD⊥AO于D,连接OC,
∴∠CDA=∠BOA=90°,
∴OB∥CD,
∴△AOB∽△ADC,
∴
=
,
∵BC=2AB,
∴AC=3AB,
∴AD=3AO,
∴AO:OD=1:2,
∵点C在双曲线y=
,
∴S△OCD=5,
∴S△AOC=
S△COD=
,
∴S△AOD=5+
=
,
∵
=(
)2,
∴S△AOB=
S△ACD=
×
=
.
故答案为:
.
 解:过点C作CD⊥AO于D,连接OC,
解:过点C作CD⊥AO于D,连接OC,∴∠CDA=∠BOA=90°,
∴OB∥CD,
∴△AOB∽△ADC,
∴
| AO |
| AD |
| AB |
| AC |
∵BC=2AB,
∴AC=3AB,
∴AD=3AO,
∴AO:OD=1:2,
∵点C在双曲线y=
| 10 |
| x |
∴S△OCD=5,
∴S△AOC=
| 1 |
| 2 |
| 5 |
| 2 |
∴S△AOD=5+
| 5 |
| 2 |
| 15 |
| 2 |
∵
| S△AOB |
| S△ACD |
| AB |
| AC |
∴S△AOB=
| 1 |
| 9 |
| 1 |
| 9 |
| 15 |
| 2 |
| 5 |
| 6 |
故答案为:
| 5 |
| 6 |
点评:此题考查了反比例函数的性质,相似三角形的判定与性质以及三角形面积问题.此题综合性较强,注意数形结合思想的应用.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )
如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )| A、3 | ||
B、
| ||
C、
| ||
D、-
|
 如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式
如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式| 1 |
| 2 |
| A、x<2 |
| B、x>-1 |
| C、x<1或x>2 |
| D、-1<x<2 |
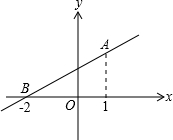 如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为
如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为 7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( )
7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( ) 16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为
16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为