题目内容
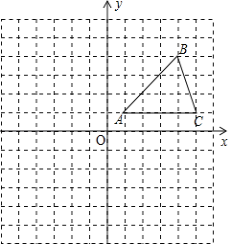
【题目】已知,如图:反比例函数y=![]() 的图象经过点A(﹣3,b)过点A作x轴的垂线,垂足为B,S△AOB=3.
的图象经过点A(﹣3,b)过点A作x轴的垂线,垂足为B,S△AOB=3.
(1)求k,b的值;
(2)若一次函数y=ax+1的图象经过点A,且与x轴交于M,求AM的长.

【答案】(1)2(2)2![]()
【解析】分析:(1)根据S△OBD=4,可求出k的值,继而求出反比例函数的解析式;
(2)将A点代入解析式,求出a的值,然后根据勾股定理可求AM得长.
详解:(1)∵S△A0B=![]() |xy|=
|xy|=![]() |k|=3,
|k|=3,
∴|k|=6,
∵反比例函数图象位于第二、四象限,
∴k<0,
∴k=﹣6,
∵反比例函数y=![]() 的图象经过点A(﹣3,b),
的图象经过点A(﹣3,b),
∴k=﹣3×b=﹣6,
解得b=2;
(2)把点A(﹣3,2)代入一次函数y=ax+1得,﹣3a+1=2,
解得a=﹣![]() ,
,
∴一次函数解析式为y=﹣![]() x+1,
x+1,
令y=0,则﹣![]() x+1=0,
x+1=0,
解得x=3,
所以,点M的坐标为(3,0),
∴AM=![]() =
=![]() =2
=2![]() .
.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目