题目内容
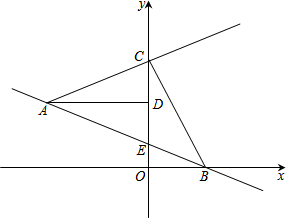 如图,一次函数y=mx+3+4m(m<0)的图象经过定点A,与x轴交于点B,与y轴交于点E,AD⊥y轴于点D,将射线AB沿直线AD翻折,交y轴于点C.
如图,一次函数y=mx+3+4m(m<0)的图象经过定点A,与x轴交于点B,与y轴交于点E,AD⊥y轴于点D,将射线AB沿直线AD翻折,交y轴于点C.
(1)用含m的代数式分别表示点B,点E的坐标;
(2)若△ABC中AC边上的高为5,求m的值;
(3)若点P为线段AC中点,是否存在m的值,使△APD与△ABD相似?若存在,请求出m的值;若不存在,请说明理由.
解:(1)∵当y=0时,mx+3+4m=0,
∴x=-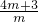 ,
,
∴B(-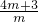 ,0).
,0).
∵当x=0时,y=3+4m,
∴E(0,3+4m);
(2)∵由直线y=mx+3+4m经过定点A,
∴定点A(-4,3).
又∵AD⊥y轴,
∴D(0,3).
由翻折可知:CD=ED=3-(4m+3)=-4m,
∴CE=2CD=-8m.
当点B在原点右边时,
S△ABC=S△ACE+S△BCE= •CE•(AD+OB)
•CE•(AD+OB)
= ×(-8m)×[4+(-
×(-8m)×[4+(-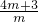 )]=
)]= ×(-8m)×(-
×(-8m)×(- )=12.
)=12.
当点B在原点左边时,
S△ABC=S△ACE-S△BCE= ×(-8m)×[4-
×(-8m)×[4-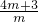 ]=
]= ×(-8m)×(-
×(-8m)×(- )=12.
)=12.
∴S△ABC=12是不变化的.
∵AC边上的高为5,
∴ AC×5=12,
AC×5=12,
∴AC=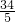 .
.
∵AD=4,∠ADC=90°,CD=-4m,
∴(-4m)2+42=( )2,解得 m=±
)2,解得 m=±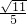 ,
,
又∵m<0,
∴m=-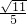 ;
;
(3)存在m的值,使△APD与△ABD相似.
①当点B在原点右边时,只有△APD∽△ADB一种情形.
∵AP=PD,
∴AD=DB=4.
∵OD=3,∴OB= ,
,
∴-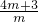 =
= ,解得 m=
,解得 m=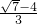 .
.
②当点B在原点左边时,
若△APD∽△ABD时,AB=DB,∴-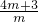 =-2,解得 m=-
=-2,解得 m=- .
.
若△APD∽△ADB时,AD=DB=4,
∵OD=3,
∴OB= ,
,
∴-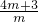 =-
=- ,解得m=-
,解得m=- .
.
∴存在m的值,使△APD与△ABD相似,m的值为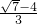 或-
或- 或-
或-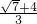 .
.
分析:(1)先令y=0求出x的值,再令x=0求出y的值即可得出B、E两点的坐标;
(2)由直线y=mx+3+4m经过定点A可得出定点A的坐标,再由AD⊥y轴可知D点坐标,根据图形翻折变换的性质可CD=ED,故可得出CE的长,当点B在原点右边时,S△ABC=S△ACE+S△BCE= •CE•(AD+OB)可得出三角形的面积;当点B在原点左边时,S△ABC=S△ACE-S△BCE可得出三角形的面积;再根据AC边上的高为5可得出AC的长,在Rt△ACD中根据勾股定理可求出m的值.
•CE•(AD+OB)可得出三角形的面积;当点B在原点左边时,S△ABC=S△ACE-S△BCE可得出三角形的面积;再根据AC边上的高为5可得出AC的长,在Rt△ACD中根据勾股定理可求出m的值.
(3)①当点B在原点右边时,只有△APD∽△ADB一种情形.因为AP=PD,所以AD=DB,再由OD的长可知OB的长,故可得出m的值;
②当点B在原点左边时,若△APD∽△ABD时,AB=DB;若△APD∽△ADB时,根据AD=DB可得出m的值.
点评:本题考查的是一次函数综合题,涉及到相似三角形的判定与性质、图形反折变换的性质、三角形的面积公式等相关知识,难度较大.
∴x=-
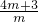 ,
,∴B(-
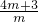 ,0).
,0).∵当x=0时,y=3+4m,
∴E(0,3+4m);
(2)∵由直线y=mx+3+4m经过定点A,
∴定点A(-4,3).
又∵AD⊥y轴,
∴D(0,3).
由翻折可知:CD=ED=3-(4m+3)=-4m,
∴CE=2CD=-8m.
当点B在原点右边时,
S△ABC=S△ACE+S△BCE=
 •CE•(AD+OB)
•CE•(AD+OB)=
 ×(-8m)×[4+(-
×(-8m)×[4+(-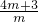 )]=
)]= ×(-8m)×(-
×(-8m)×(- )=12.
)=12.当点B在原点左边时,
S△ABC=S△ACE-S△BCE=
 ×(-8m)×[4-
×(-8m)×[4-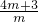 ]=
]= ×(-8m)×(-
×(-8m)×(- )=12.
)=12.∴S△ABC=12是不变化的.
∵AC边上的高为5,
∴
 AC×5=12,
AC×5=12,∴AC=
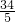 .
.∵AD=4,∠ADC=90°,CD=-4m,
∴(-4m)2+42=(
 )2,解得 m=±
)2,解得 m=±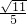 ,
,又∵m<0,
∴m=-
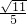 ;
;(3)存在m的值,使△APD与△ABD相似.
①当点B在原点右边时,只有△APD∽△ADB一种情形.
∵AP=PD,
∴AD=DB=4.
∵OD=3,∴OB=
 ,
,∴-
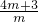 =
= ,解得 m=
,解得 m=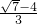 .
.②当点B在原点左边时,
若△APD∽△ABD时,AB=DB,∴-
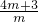 =-2,解得 m=-
=-2,解得 m=- .
.若△APD∽△ADB时,AD=DB=4,
∵OD=3,
∴OB=
 ,
,∴-
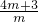 =-
=- ,解得m=-
,解得m=- .
.∴存在m的值,使△APD与△ABD相似,m的值为
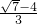 或-
或- 或-
或-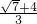 .
.分析:(1)先令y=0求出x的值,再令x=0求出y的值即可得出B、E两点的坐标;
(2)由直线y=mx+3+4m经过定点A可得出定点A的坐标,再由AD⊥y轴可知D点坐标,根据图形翻折变换的性质可CD=ED,故可得出CE的长,当点B在原点右边时,S△ABC=S△ACE+S△BCE=
 •CE•(AD+OB)可得出三角形的面积;当点B在原点左边时,S△ABC=S△ACE-S△BCE可得出三角形的面积;再根据AC边上的高为5可得出AC的长,在Rt△ACD中根据勾股定理可求出m的值.
•CE•(AD+OB)可得出三角形的面积;当点B在原点左边时,S△ABC=S△ACE-S△BCE可得出三角形的面积;再根据AC边上的高为5可得出AC的长,在Rt△ACD中根据勾股定理可求出m的值.(3)①当点B在原点右边时,只有△APD∽△ADB一种情形.因为AP=PD,所以AD=DB,再由OD的长可知OB的长,故可得出m的值;
②当点B在原点左边时,若△APD∽△ABD时,AB=DB;若△APD∽△ADB时,根据AD=DB可得出m的值.
点评:本题考查的是一次函数综合题,涉及到相似三角形的判定与性质、图形反折变换的性质、三角形的面积公式等相关知识,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知,如图,一次函数y1=-x-1与反比例函数y2=-
已知,如图,一次函数y1=-x-1与反比例函数y2=-| 2 |
| x |
| A、x>1 |
| B、x<-2或0<x<1 |
| C、-2<x<1 |
| D、-2<x<0或x>1 |
 如图,一次函数y=kx+2的图象与反比例函数y=
如图,一次函数y=kx+2的图象与反比例函数y= 13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是
13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是 (2013•成都)如图,一次函数y1=x+1的图象与反比例函数
(2013•成都)如图,一次函数y1=x+1的图象与反比例函数 如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数
如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数