题目内容
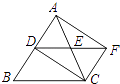
【题目】如图,△ABC的三条角平分线相交于点I,过点I作DI⊥IC,交AC于点D.
(1)如图①,求证:∠AIB=∠ADI;
(2)如图②,延长BI,交外角∠ACE的平分线于点F.
①判断DI与CF的位置关系,并说明理由;
②若∠BAC=70°,求∠F的度数.


【答案】(1)证明见解析;(2)解:①结论:DI∥CF,②35°.
【解析】(1)只要证明∠AIB=90°+![]() ∠ACB,∠ADI=90°+
∠ACB,∠ADI=90°+![]() ∠ACB即可;
∠ACB即可;
(2)①只要证明∠IDC=∠DCF即可;
②首先求出∠ACE-∠ABC=∠BAC=70°,再证明∠F=![]() ∠ACE-
∠ACE-![]() ∠ABC=
∠ABC=![]() (∠ACE-∠ABC)即可解决问题;
(∠ACE-∠ABC)即可解决问题;
(1)证明:∵AI,BI分别平分∠BAC,∠ABC,
∴∠BAI=![]() ∠BAC,∠ABI=
∠BAC,∠ABI=![]() ∠ABC,
∠ABC,
∴∠BAI+∠ABI=![]() (∠BAC+∠ABC)=
(∠BAC+∠ABC)=![]() (180°-∠ACB)=90°-
(180°-∠ACB)=90°-![]() ∠ACB.
∠ACB.
在△ABI中,∠AIB=180°-(∠BAI+∠ABI)=180°-(90°-![]() ∠ACB)=90°+
∠ACB)=90°+![]() ∠ACB.
∠ACB.
∵CI平分∠ACB,∴∠DCI=![]() ∠ACB.∵DI⊥IC,
∠ACB.∵DI⊥IC,
∴∠DIC=90°,∴∠ADI=∠DIC+∠DCI=90°+![]() ∠ACB.
∠ACB.
∴∠AIB=∠ADI.
(2)解:①结论:DI∥CF.
理由:∵∠IDC=90°-∠DCI=90°-![]() ∠ACB,CF平分∠ACE,
∠ACB,CF平分∠ACE,
∴∠ACF=![]() ∠ACE=
∠ACE=![]() (180°-∠ACB)=90°-
(180°-∠ACB)=90°-![]() ∠ACB,∴∠IDC=∠ACF,∴DI∥CF.
∠ACB,∴∠IDC=∠ACF,∴DI∥CF.
②∵∠ACE=∠ABC+∠BAC,∴∠ACE-∠ABC=∠BAC=70°.
∵∠FCE=∠FBC+∠F,∴∠F=∠FCE-∠FBC.
∵∠FCE=![]() ∠ACE,∠FBC=
∠ACE,∠FBC=![]() ∠ABC,
∠ABC,
∴∠F=![]() ∠ACE-
∠ACE-![]() ∠ABC=
∠ABC=![]() (∠ACE-∠ABC)=35°.
(∠ACE-∠ABC)=35°.

 智慧小复习系列答案
智慧小复习系列答案【题目】在某项针对18﹣35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,m≥15时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,制作图表如下: 18﹣35岁青年人日均发微博条数统计表
m | 频数 | 百分数 |
A级(0≤m<5) | 90 | 0.3 |
B级(5≤m<10) | 120 | a |
C级(10≤m<15) | b | 0.2 |
D级(m≥15) | 30 | 0.1 |
请你根据以上信息解答下列问题:
(1)求a,b;
(2)补全频数分布直方图.