题目内容
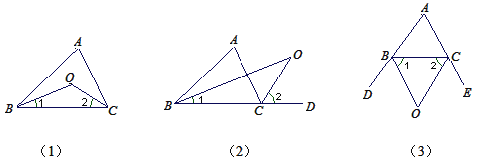
【题目】如图（1）所示，△ABC中，∠ABC，∠ACB的平分线交于点O，求证：∠BOC=90+
∠A．
变式1：如图（2）所示，∠ABC，∠ACD的平分线交于点O，求证：∠BOC=∠A．
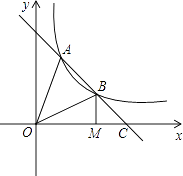
变式2：如图（3）所示，∠CBD，∠BCE的平分线交于点O，求证：∠BOC=90-∠A．
【答案】见解析
【解析】
（1）先根据三角形内角和定理得到∠BOC=180°-∠OBC-∠OCB，则2∠BOC=360°-2∠OBC-2∠OCB，再根据角平分线的定义得∠ABC=2∠OBC，∠ACB=2∠OCB，则2∠BOC=360°-∠ABC-∠ACB，易得∠BOC=90°+
∠A；
变式1：根据BD为△ABC的角平分线，CD为△ABC外角∠ACE的平分线，由三角形外角性质可得；∠2=∠1+∠O，∠ACO=∠2=∠ACD=(∠A+∠ABC)=(∠A+2∠1) =∠A+∠1，两式联立可得 ∠1+∠O = ∠A+∠1，即∠BOC=∠A．
变式2：根据三角形外角平分线的性质可得∠BCO= （∠A+∠ABC）、∠OBC= （∠A+∠ACB）；根据三角形内角和定理可得∠BOC=90-∠A..
（1）证明：在△BOC中，
∵∠BOC=180°-∠OBC-∠OCB，
∴2∠BOC=360°-2∠OBC-2∠OCB，
∵BO平分∠ABC，CO平分∠ACB，
∴∠ABC=2∠OBC，∠ACB=2∠OCB，
∴2∠BOC=360°-（∠ABC+∠ACB），
∵∠ABC+∠ACB=180°-∠A，
∴2∠BOC=180°+∠A，
∴∠BOC=90°+∠A；
变式1：∵BD为△ABC的角平分线，CD为△ABC外角∠ACE的平分线，
∴ ∠1= ∠ABC ∠ACO=∠2=∠ACD
∵∠2、∠ACO分别是△BCO、△ABC的外角
∴∠2=∠1+∠O，∠ACO=∠2=∠ACD=(∠A+∠ABC)=(∠A+2∠1) =∠A+∠1，
∴ ∠1+∠O = ∠A+∠1，
∴∠BOC=∠A．
变式2：∵BO、CO为△ABC中∠ABC、∠ACB的外角平分线.
∴∠BCO= （∠A+∠ABC）、∠OBC= （∠A+∠ACB），
由三角形内角和定理得，∠BOC=180°-∠BCO-∠OBC，
=180°- [∠A+（∠A+∠ABC+∠ACB）]，
=180°- （∠A+180°），
=90°- ∠A；
